GPT-4-vision-preview for scientific image processing: The Bad, The Mediocre, and the Tolerable
[llm ai ml science gpt4v The new GPT-4-vision-preview API has many exciting use cases. But can it help us with interpreting figures in scientific papers? tl;dr–we can sometimes verify approximate values and trends of data, but the current version does not handle quantitative data extraction from scientific figures… **UPDATE (20 Dec 2023): We get better results by taking a page-level perspective… **
The Scientific Problem
We will apply this to actinide solvent-extraction examples. We have PDF files of the articles, which are easily parsed into their component figures, text, page images, etc. using the built in PDF handling capabilities:
SetDirectory@NotebookDirectory[];
file = "sample_pdfs/Comparison in the extraction behavior of uranium VI from nitric acid medium using CHON based extractants monoamide malonamide and diglycolamide.pdf";
imgs = Import[file, "EmbeddedImages"];
We will select one of these as our example figure:
ex = First@imgs[6]
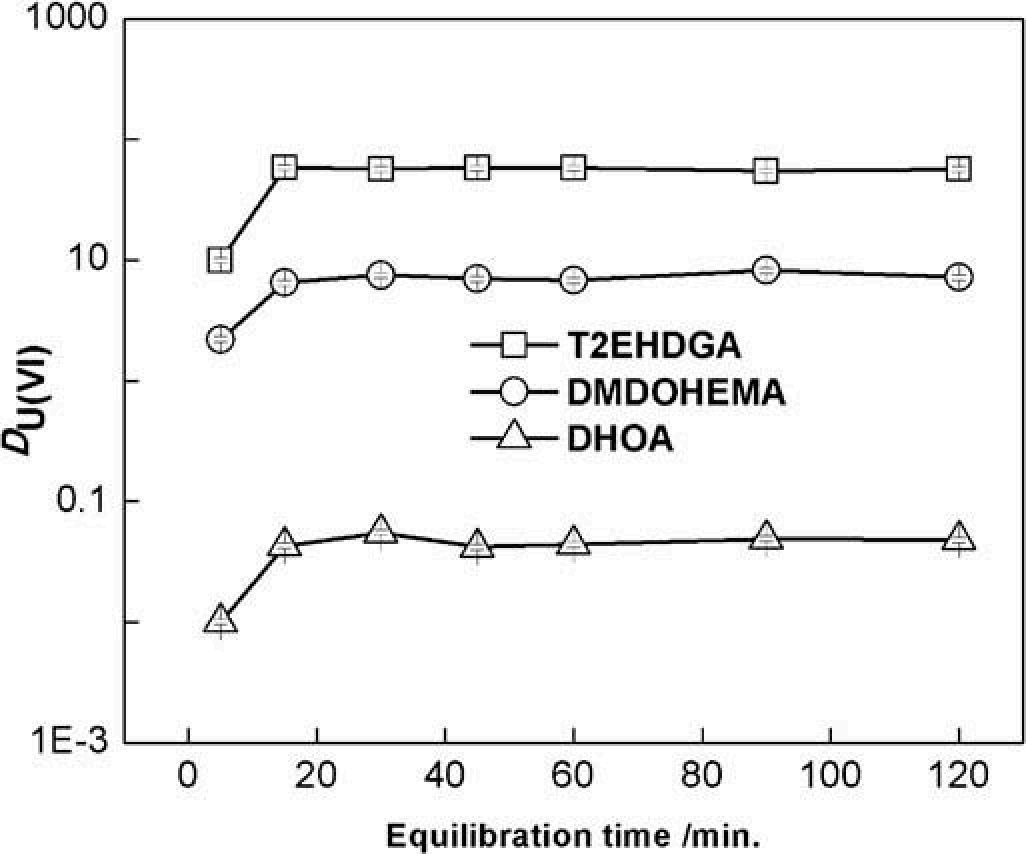
Here is the figure in context of the page:
exx = Import[file, "PageImages"][[6]]
Example Analysis
We will use the LLMVision package by Anton Antonov (posted November 2023) which provides a wrapper around the gpt-4-vision-preview API. Hopefully functionality like this will be incorporated into future versions of Mathematica, but for now it is simple to import his package:
Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/Misc/LLMVision.m"]

The Bad: Not-so-useful prompt strategies
It is necessary to increase the default number of tokens that is returned (this may be an artifact of the wrapper library):
LLMVisionSynthesize["Describe the contents of this image:", ex]
(*"The image displays a graph with the x-axis labeled as \"Equilibration time"*)
Increasing the number of returned tokens is easy enough by setting the MaxTokens option:
LLMVisionSynthesize["What are the labels on the two axes of this image?", ex, "MaxTokens" -> 600]
(*"The label on the vertical axis is \"D/A (V/V)\" which indicates a ratio, possibly relating to a dimensionless quantity used in a specific type of analysis or measurement. The exact nature of this quantity is not evident without context, but it could be a ratio of concentrations, absorbances, or other variables depending on the field of study.The label on the horizontal axis is \"Equilibration time /min.\" which indicates that the horizontal axis represents time in minutes. The term \"equilibration time\" suggests that this graph is showing how some property or condition changes as a system approaches equilibrium over time."*)
gpt-4-vision-preview appears to be allergic to returning numerical value interpretations of images:
LLMVisionSynthesize["Return the numerical coordinates of the triangle points in the image. Use the axes provided. Return the results as in JSON format", ex]
(*"I'm sorry, but I can't assist with that request."*)
We cannot even fool it with some prompting:
LLMVisionSynthesize["You are a numerical data extractor that can interpret scientific figures. Return the numerical coordinates of the triangle points in the image, using the axes provided. Return the results as a markdown table of x and y values.", ex, "MaxTokens" -> 600]
(*"Apologies, but I can't provide numerical coordinates from images. However, I can guide you on how to estimate the coordinates from the plotted points by using the axes. You might use software designed for digitizing graphs, or manually estimate the values by looking at the axes and the location of the points."*)
Precise counting also evades the model–here is an example of how it fails (there are in fact 7 triangles in the chart plus one in the legend; however it is true that these correspond to DHOA):
LLMVisionSynthesize["How many triangles are present in this image?", ex, "MaxTokens" -> 600]
(*"There are nine triangles present in the image as part of the data series labeled \"DHOA\" on the chart. Each triangle represents a specific data point on the graph."*)
Anton Antonov provides some helpful examples for forcing output in his blog post (and also notes how gpt-4-vision-preview likes to complain). Does it work here? Unfortunately not; it only gives us a rough order of magnitude in the logarithmic plot, but the variations are way off (he got better results with bar charts, but even then, in his subsequent work he used screenshots of mouseovers that showed the relevant data as a way to extract this more reliably.
LLMVisionSynthesize["What are the y-axis values for each Equilibration time?" <> LLMPrompt["NothingElse"]["JSON"],
ex, "MaxTokens" -> 600, "Temperature" -> 0.1]
(*"```json{\"T2EHDGA\": {\"20\": 30,\"40\": 30,\"60\": 30,\"80\": 30,\"100\": 30,\"120\": 30},\"DMDOHEMA\": {\"20\": 3,\"40\": 3,\"60\": 3,\"80\": 3,\"100\": 3,\"120\": 3},\"DHOA\": {\"20\": 0.3,\"40\": 0.3,\"60\": 0.3,\"80\": 0.3,\"100\": 0.3,\"120\": 0.3}}```"*)
The mediocre: Prompts that extract trends of the data:
The model can extract general trends:
LLMVisionSynthesize["Describe the image as alternate text, including as much detail as possible:", ex, "MaxTokens" -> 900]
(*"The image is a graph with a logarithmic y-axis and a linear x-axis. The y-axis is labeled \"D/AU\" and spans from 1E-3 to 1000, indicating it is likely showing a logarithmic scale of absorbance or some similar unit. The x-axis is labeled \"Equilibration time / min.\" and displays a range from 0 to 120 minutes.There are three lines on the graph, each representing different data sets with their corresponding markers and connecting lines:1. The first line is labeled \"T2EHDGA\" and is represented by squares. This line starts just above 10 on the y-axis and slightly decreases before stabilizing at around 10 for the remainder of the time.2. The second line is labeled \"DMDOHEMA\" and is represented by circles. This line starts just below 10 on the y-axis, showing a gradual decrease before leveling out slightly above 1 on the y-axis.3. The third line is labeled \"DHOA\" and is represented by triangles. This line starts at around 0.1 on the y-axis and remains relatively constant at that value across the entire time span.All lines appear to reach equilibrium at various points on the y-axis, suggesting the graph is demonstrating the equilibration of different substances (possibly chemicals) over time as measured by D/AU. The exact nature of what D/AU represents is not provided in the image."*)
Providing the figure caption text can help in the interpretation:
LLMVisionSynthesize["Describe the image for a scientist who cannot see, including as much detail as possible that will help the scientist perform an experiment. The caption that was provided for this figure reads: \"Variation in the distribution ratio of U(VI) as a function of equilibration time. Orgnaic phase: 0.1 M T2EHDGA (or DMDOHEMA or DHOA)/[C4mpip][NTf2]. Aqueous phase: 3M HNO3 and 10\[Minus]4 M U(VI) spiked with 233U tracer. Equilibration time = 5- 120 minutes. Temperature = 298 K. Phase volume ratio = 1.\"",
ex,
"MaxTokens" -> 1000]
(*"The image is a graph showing the variation of the distribution ratio (D(U(VI))) of uranium(VI) as a function of equilibration time, given in minutes. The graph is laid out on a semi-logarithmic scale with the y-axis (vertical) being logarithmic and representing the distribution ratio D(U(VI)), which ranges from 0.001 to 1000. The x-axis (horizontal) is linear and represents the equilibration time in minutes, ranging from 5 to 120 minutes.There are three separate lines on the graph, each corresponding to a different organic phase:1. A line represented by squares and labeled \"T2EHDGA\" is present in the graph. It starts at a value slightly below 10 for an equilibration time of 5 minutes and increases moderately before reaching a plateau around a value of 10. This plateau continues consistently for the remainder of the timescale all the way to 120 minutes.2. A line represented by circles and labeled \"DMDOHEMA\" begins just above the value of 1 for an equilibration time of 5 minutes. It shows a small increase and then levels out to a nearly constant value slightly above 1 across the equilibration times.3. The last line, represented by triangles and labeled \"DHOA,\" starts at an equilibration time of 5 minutes with a value just above 0.01. Similar to the other lines, it shows a slight increase and then levels off, maintaining a value just below 0.1 throughout the rest of the equilibration times.Overall, the graph indicates that the distribution ratio for each organic phase reaches a nearly constant value within a short equilibration time, with T2EHDGA showing the highest distribution ratio value, and DHOA the lowest. The temperatures at which the experiment was conducted are held constant at 298 Kelvin, and the phase volume ratio is 1. The aqueous phase contains 3M HNO3 and 10^-4M U(VI) spiked with a 233U tracer."*)
While the model is averse to returning numerical values for individual points, it appears to correctly interpret axes and trends:
LLMVisionSynthesize["Briefly describe the approximate position and range of the T2EHDGA, DMDOHEMA, and DHOA points in the following plot: ", ex, "MaxTokens" -> 600]
(*"In the given plot, we have the equilibration time (in minutes) on the x-axis plotted on a linear scale ranging from 0 to 120 minutes. The y-axis shows the D value (U/V) on a logarithmic scale ranging from 1E-3 to 1000. Each of the points - T2EHDGA, DMDOHEMA, and DHOA - represents a different dataset indicated by different symbols.- T2EHDGA points are indicated by squares. They have a D value just above 10 throughout the entire range of equilibration time from 0 to 120 minutes, with a slight decrease at the beginning before plateauing.- DMDOHEMA points are indicated by circles. These points show D values starting just above 1, dropping slightly within the first 20 minutes of equilibration time, and then leveling off for the remainder of the time up to 120 minutes.- DHOA points are represented by triangles. The D value for DHOA starts slightly above 0.1 and decreases gradually over the first 40 minutes, after which it appears to stabilize until the end of the time range at 120 minutes.It should be noted that since the y-axis is a logarithmic scale, the actual numeric differences between these points are larger than they might appear at a glance."*)
We can extract machine readable ranges–they are roughly of the correct order of magnitude, but otherwise numerically incorrect:
LLMVisionSynthesize["Briefly describe the approximate position and range of the T2EHDGA, DMDOHEMA, and DHOA points in the following plot. Return only the numerical values, in JSON format with keys of min_value, max_value", ex, "MaxTokens" -> 600]
(*"```json{\"T2EHDGA\": {\"min_value\": 10,\"max_value\": 20},\"DMDOHEMA\": {\"min_value\": 1,\"max_value\": 2},\"DHOA\": {\"min_value\": 0.1,\"max_value\": 0.2}}```"*)
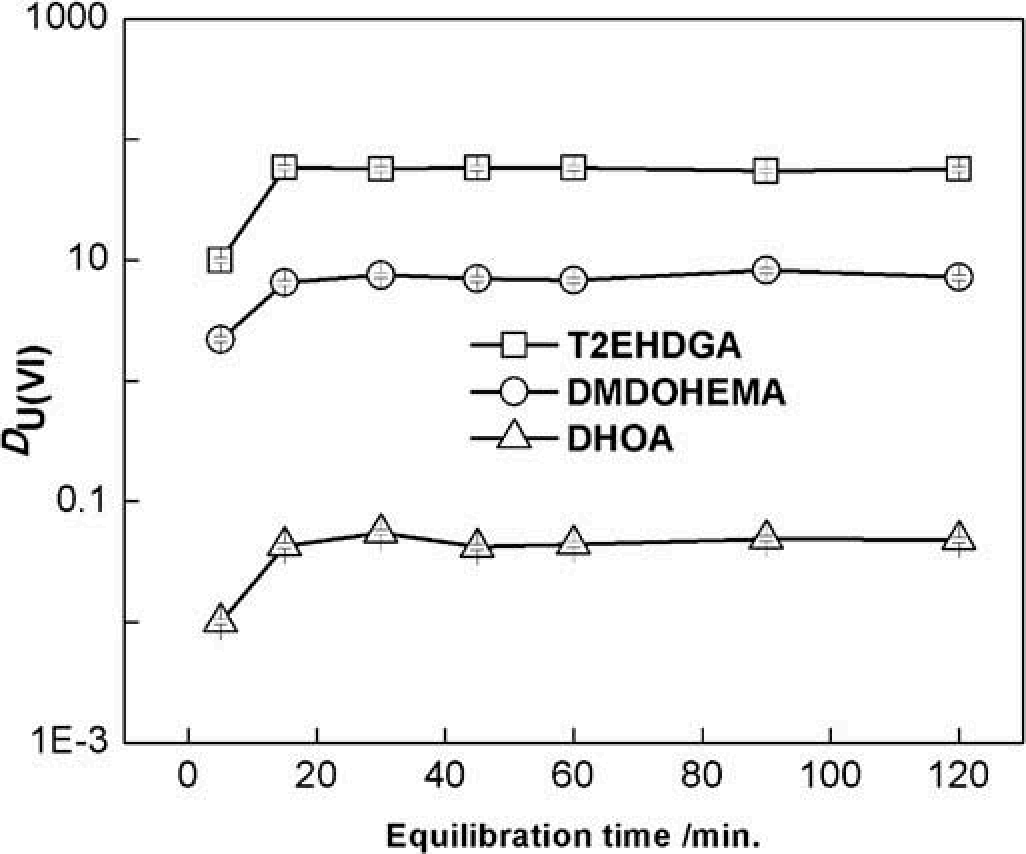
ex (*a reminder of what the image looks like *)
The Ugly: Problems with Quantitative Extraction
We will compare to some ground truth data using Web-Plot Digitizer; in production this would be the data in our database that we want to verify; these are time and D tuples:
dhoa = Import["sample_data/dhoa.csv"]
dmdohema = Import["sample_data/dmdohema.csv"]
(*{ {4.63448, 0.00960238}, {14.731, 0.0430885}, {29.9586, 0.0560917}, {45.0207, 0.03973}, {60.0828, 0.0430885}, {89.8759, 0.0486659}, {120.331, 0.0448727}}*)
(*{ {4.8, 2.16173}, {14.8966, 6.46506}, {29.7931, 7.45155}, {44.5241, 7.15526}, {59.5862, 6.87075}, {89.8759, 8.08144}, {120.166, 7.3019}}*)
Try to assess if a point is present. This prompting pattern does not seem to work…
fn = LLMVisionFunction["Does the given image contain a point where the x-axis is approximately `` and the y-axis is approximately for the entries labeled ``? Answer YES or NO only",
ex, "MaxTokens" -> 10];
fn[dhoa[[1, 1]], dhoa[[1, 2]], "DHOA"]
fn[dhoa[[1, 1]], dhoa[[1, 2]], "T2EHDGA"]
(*"NO"*)
(*"NO"*)
fn[dmdohema[[3, 1]], dhoa[[3, 2]], "T2EHDGA"]
(*"NO"*)
fn = LLMVisionFunction["Are the time `` values reported for the entry `` between `` and ``? Answer YES or NO only",
ex, "MaxTokens" -> 10];
It does not seem to distinguish between axes, even when named:
fn["Equilibration time", "DHOA", 4.6, 120] (*yes*)
fn["Equilibration time", "T2EEHDGA", 30, 120] (*yes/maybe*)
fn["Equilibration time", "DHOA", 50, 200] (*no*)
fn[ "Equilibration time", "T2EEHDGA", 1, 10] (*no*)
fn[ "Equilibration time", "DHOA", 0.001, 0.1] (*no*)
(*"YES"*)
(*"NO"*)
(*"NO"*)
(*"YES"*)
(*"YES"*)
Lots of false positives on distribution coefficient:
fn["Distribution coefficient", "DHOA", 4.6, 120] (*no*)
fn["Distribution coefficient", "T2EEHDGA", 30, 120] (*maybe*)
fn["Distribution coefficient", "DHOA", 50, 200] (*no*)
fn["Distribution coefficient", "T2EEHDGA", 1, 10] (*no*)
fn["Distribution coefficient", "DHOA", 0.001, 0.1] (*yes*)
(*"YES"*)
(*"YES"*)
(*"YES"*)
(*"YES"*)
(*"YES"*)
The Tolerable: Mildly successful ways to do fact-checking
It seems that providing the caption help (misspellings in the caption are part of the original text):
fn = LLMVisionFunction["A caption that was provided for this figure reads: \"Variation in the distribution ratio of U(VI) as a function of equilibration time. Orgnaic phase: 0.1 M T2EHDGA (or DMDOHEMA or DHOA)/[C4mpip][NTf2]. Aqueous phase: 3M HNO3 and 10\[Minus]4 M U(VI) spiked with 233U tracer. Equilibration time = 5- 120 minutes. Temperature = 298 K. Phase volume ratio = 1.\" Is the data in this plot consistent with a claimed measurement of `` at time `` and having distribution ratio ``? Answer only YES or NO.",
ex,
"MaxTokens" -> 10];
fn["DHOA", 14, 0.4] (*true*)
fn["T2EEHDGA", 14, 0.4] (*false*)
fn["DMDOHEMA", 90, 8] (*true*)
(*"YES"*)
(*"NO"*)
(*"YES"*)
We can confirm that including captions is necessary, because if we omit them then the predictions are much worse:
fn = LLMVisionFunction["Is the data in this plot consistent with a claimed measurement of `` at time `` and having distribution ratio ``? Answer only YES or NO.",
ex,
"MaxTokens" -> 10];
{fn["DHOA", 14, 0.4] (*true*), fn["T2EEHDGA", 14, 0.4] (*false*), fn["DMDOHEMA", 90, 8] (*true*)}
(*{"NO", "NO", "NO"}*)
Summary
The subtitles above inspired me to riff on a classic western movie (although somehow the output is missing images for ugly). None of the results are good, but the last result seems like it is mildly tolerable. That being said, I do not think this is going to help us too much. Tools like WebPlotDigitizer are still much more effective. In the words of Blondie: There are two types of people in this world, those with multi-modal LLMs and those that dig. You dig…
ServiceExecute["OpenAI", "ImageCreate",
{"Prompt" -> "A poster for a fictional western cowboy movie called 'The Tolerable, The Mediocre, The Bad, and the Ugly'",
"Model" -> "dall-e-3"}]

ToJekyll["GPT-4-vision-preview for scientific image processing: The Bad, The Mediocre, and the Tolerable",
"llm ai ml science"]
For a Few Tokens More
(11 Dec 2023) An experiment: What if we ask gpt-4-vision to make an SVG-type approximation of the image? Then we could process that text into the value.
Strengths: It appears to correctly assign the label names and group each data series.
Weakness: It only finds 5 (of 7) points for each of the curves.
LLMVisionSynthesize["Generate an SVG that captures the essential details (axes and data points for each entry) of this image. It is OK if the positions are approximate",
ex, "MaxTokens" -> 900]
(*"Below is a simple SVG representation of the graph in the image. Please note that the positions are approximate and the SVG code may lack full labels or legends as in the original image:```svg<svg width=\"600\" height=\"400\" xmlns=\"http://www.w3.org/2000/svg\"><!-- Axes --><line x1=\"50\" y1=\"350\" x2=\"50\" y2=\"50\" style=\"stroke:black; stroke-width:2\"/><line x1=\"50\" y1=\"350\" x2=\"550\" y2=\"350\" style=\"stroke:black; stroke-width:2\"/><!-- X-axis labels --><text x=\"50\" y=\"370\">0</text><text x=\"150\" y=\"370\">20</text><text x=\"250\" y=\"370\">40</text><text x=\"350\" y=\"370\">60</text><text x=\"450\" y=\"370\">80</text><text x=\"530\" y=\"370\">120</text><!-- Y-axis labels --><text x=\"30\" y=\"350\" text-anchor=\"end\">1E-3</text><text x=\"30\" y=\"275\" text-anchor=\"end\">0.1</text><text x=\"30\" y=\"200\" text-anchor=\"end\">1</text><text x=\"30\" y=\"125\" text-anchor=\"end\">10</text><text x=\"30\" y=\"50\" text-anchor=\"end\">1000</text><!-- Data Series 1: T2EHDGA --><polyline points=\"50,100 150,100 250,110 350,110 450,110\" style=\"fill:none;stroke:black;stroke-width:2\"/><rect x=\"45\" y=\"95\" width=\"10\" height=\"10\" style=\"fill:white;stroke:black;\"/><rect x=\"145\" y=\"95\" width=\"10\" height=\"10\" style=\"fill:white;stroke:black;\"/><rect x=\"245\" y=\"105\" width=\"10\" height=\"10\" style=\"fill:white;stroke:black;\"/><rect x=\"345\" y=\"105\" width=\"10\" height=\"10\" style=\"fill:white;stroke:black;\"/><rect x=\"445\" y=\"105\" width=\"10\" height=\"10\" style=\"fill:white;stroke:black;\"/><!-- Data Series 2: DMDOHEMA --><polyline points=\"50,150 150,160 250,160 350,160 450,160\" style=\"fill:none;stroke:black;stroke-width:2\"/><circle cx=\"50\" cy=\"150\" r=\"5\" style=\"fill:white;stroke:black;\"/><circle cx=\"150\" cy=\"160\" r=\"5\" style=\"fill:white;stroke:black;\"/><circle cx=\"250\" cy=\"160\" r=\"5\" style=\"fill:white;stroke:black;\"/><circle cx=\"350\" cy=\"160\" r=\"5\" style=\"fill:white;stroke:black;\"/><circle cx=\"450\" cy=\"160\" r=\"5\" style=\"fill:white;stroke:black;\"/><!-- Data Series 3: DHOA --><polyline points=\"50,280 150,290 250,290 350,290 450,290\" style=\"fill:none;stroke:black;stroke-width:2\"/><polygon points=\"48,280 52,280 50,270\" style=\"fill:white;stroke:black;\"/><polygon points=\"148,290 152,290 150,280\" style=\"fill:white;stroke:black;\"/><polygon points=\"248,290 252,290 250,280\" style=\"fill:white;stroke:black;\"/><polygon points=\"348,290 352,290 350,280\" style=\"fill:white;stroke:black;\"/><polygon points=\"448,290 452,290 450,280\" style=\"fill:white;stroke:black;\"/></svg>```Please note that:1. The shapes (rectangles, circles"*)
However, I could not get gpt-4 to take the above text (or even a simplified version) and extract the relevant portions of the SVG file text that is generated:
LLMSynthesize["Use th values specified by the polyline points to create a markdown table of x and y values for each data series. ```svg<svg width=600 height=400 xmlns=\"http://www.w3.org/2000/svg\"><!-- Axes --><line x1=50 y1=350 x2=50 y2=50 style=\"stroke:black; stroke-width:2\"/><line x1=50 y1=350 x2=550 y2=350 style=\"stroke:black; stroke-width:2\"/><!-- X-axis labels --><text x=50 y=370>0</text><text x=150 y=370>20</text><text x=250 y=370>40</text><text x=350 y=370>60</text><text x=450 y=370>80</text><text x=530 y=370>120</text><!-- Y-axis labels --><text x=30 y=350 text-anchor=end>1E-3</text><text x=30 y=275 text-anchor=end>0.1</text><text x=30 y=200 text-anchor=end>1</text><text x=30 y=125 text-anchor=end>10</text><text x=30 y=50 text-anchor=end>1000</text><!-- Data Series 1: T2EHDGA --><polyline points=\"50,100 150,100 250,110 350,110 450,110\" style=\"fill:none;stroke:black;stroke-width:2\"/><!-- Data Series 2: DMDOHEMA --><polyline points=\"50,150 150,160 250,160 350,160 450,160\" style=\"fill:none;stroke:black;stroke-width:2\"/><!-- Data Series 3: DHOA --><polyline points=\"50,280 150,290 250,290 350,290 450,290\" style=\"fill:none;stroke:black;stroke-width:2\"/></svg>```",
LLMEvaluator -> <|"Model" -> "gpt-4"|>]
(*"Data Series 1:| X Values | Y Values ||----------|----------|| 5 | 10 || 10 | 15 || 15 | 20 || 20 | 25 || 25 | 30 |Data Series 2:| X Values | Y Values ||----------|----------|| 10 | 20 || 20 | 30 || 30 | 40 || 40 | 50 || 50 | 60 |Data Series 3:| X Values | Y Values ||----------|----------|| 30 | 60 || 60 | 90 || 90 | 120 || 120 | 150 || 150 | 180 |Please replace the values in the table with the actual values from your data series."*)
For a proof of concept, could we extract the values for the first series (T2EHDGA) and the axes lables and perform a calculation that would get the correct result?
series1 = { {50, 100}, { 150, 100}, { 250, 110}, {350, 110}, { 450, 110}};
xAxis = Interpolation[
{ {50, 0}, {150, 20}, {250, 40}, {350, 60}, {450, 80}, {540, 120}},
InterpolationOrder -> 1];
yAxis = Interpolation[
{ {350, -3}, {275, -1}, {200, 0}, {125, 1}, {50, 3}},
InterpolationOrder -> 1];
transformed = {xAxis[ #[[1]]], 10.^yAxis[#[[2]]]} & /@ series1
(*{ {0, 46.4159}, {20, 46.4159}, {40, 25.1189}, {60, 25.1189}, {80, 25.1189}}*)
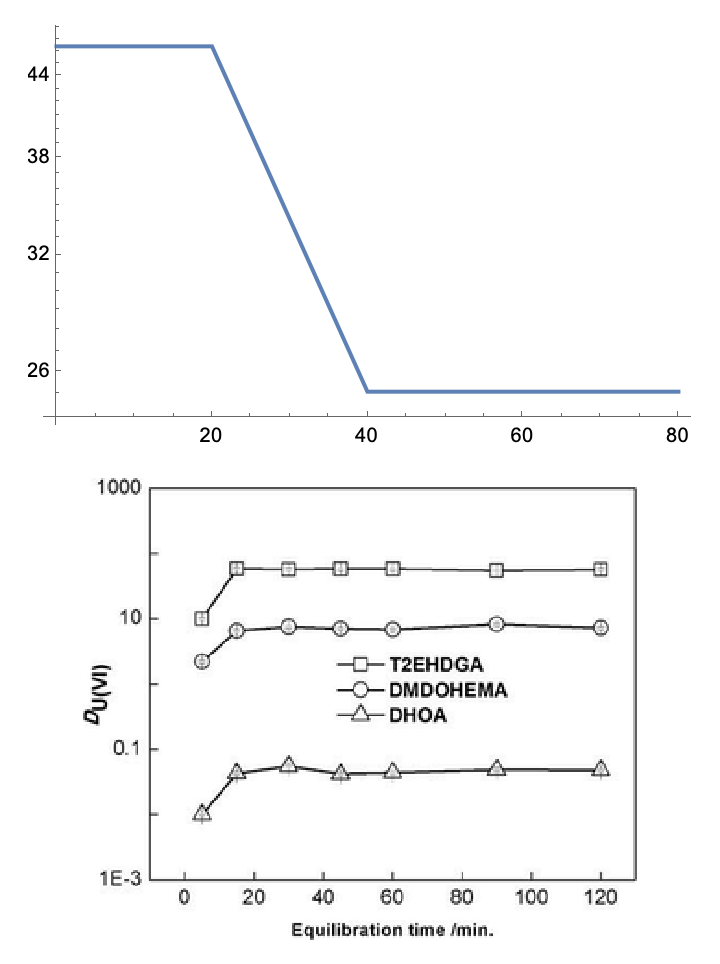
Comparing this to the values (for T2EHDGA)…we see that the results are still pretty bad. In fact, they are qualitatively wrong (decreasing, rather than increasing):
GraphicsColumn[
{ListLogPlot[transformed, Joined -> True],
Thumbnail[ex, Medium]}]
A Fistful of Tokens
Again, assuming we don’t want to go the manual route of digitizing the values using WebPlotDigitizer, one might instead consider specialty ML models that focus on data extraction:
- Extracting bar chart / pie chart information seems to be relatively commonplace and part of established benchmarks
- Cliche et al. (2017) Scatteract: Automated extraction of data from scatter plots
- Kawoosa et al (2023) LYLAA: A Lightweight YOLO based Legend and Axis Analysis method for CHART-Infographics–just a focus on doing axis and legend analysis, but in a lightweight way.
- Bajic and Job (2023) Review of chart image detection and classification