Computational Sculpture: After Karen Bexfield, part 2

Our last attempt at this project resulted in a kind of lumpy potato from the lofting effect. This suggested another approach: start with inherently conical structures. This results in a much more pleasing effect…

Interactive design

Our default unit is Imperial (inches), and we will start with two Cones that have the same radius as their height (this gives a 45 degree angle). Ultimately we want to slice off portions of each cone to achieve the desired shape; while we might think about doing this with cutting planes, there is no clear (documented) way of using those planes with OpenCascadeLink (which is our goal). So instead, we will treat the cut areas as Cuboids that extend sufficiently far away.

• Boxes 1 and 2 have a moveable z-axis

• Box 2 can also have a tilt (make this the top of the print)– we will implement this using a RotationTransform that tilts positive z-axis towards some other point with specified x and y coordinates.

• Box 3 moves along the y axis (possible improvements would be to give it a tilt)

bicone[R_] := {
    Cone[{ {0, 0, 0}, {0, 0, R}}, R], 
    Cone[{ {0, 0, 0}, {0, 0, -R}}, R]} 
 
Manipulate[
  With[
   {R = 4, 
    cubes = { Cuboid[{5, 5, z1}, {-5, -5, -5}], 
      Cuboid[{5, 5, 5}, {-5, -5, z2}], 
      Cuboid[{-5, y3, -5}, {5, 5, 5}]}, 
    rot = RotationTransform[{ {0, 0, 1}, {x2, y2, 1}}]}, 
  	
   CopyToClipboard[<|"cubes" -> cubes, "rotation" -> rot|>]; 
   Show[
    Graphics3D[
     {Red, Opacity[0.2], bicone[R], 
      Blue, Opacity[0.1], 
      cubes[[1]], 
      rot@cubes[[2]], 
      cubes[[3]] 
     }], 
    PlotRange -> { {-5, 5}, {-5, 5}, {-5, 5}}]], 
  { {z1, -3}, 0, -4}, 
  { {x2, 0}, 0, 4}, 
  { {y2, 0}, 0, 4}, 
  { {z2, 3}, 0, 4}, 
  { {y3, 3}, 0, 4} 
 ]

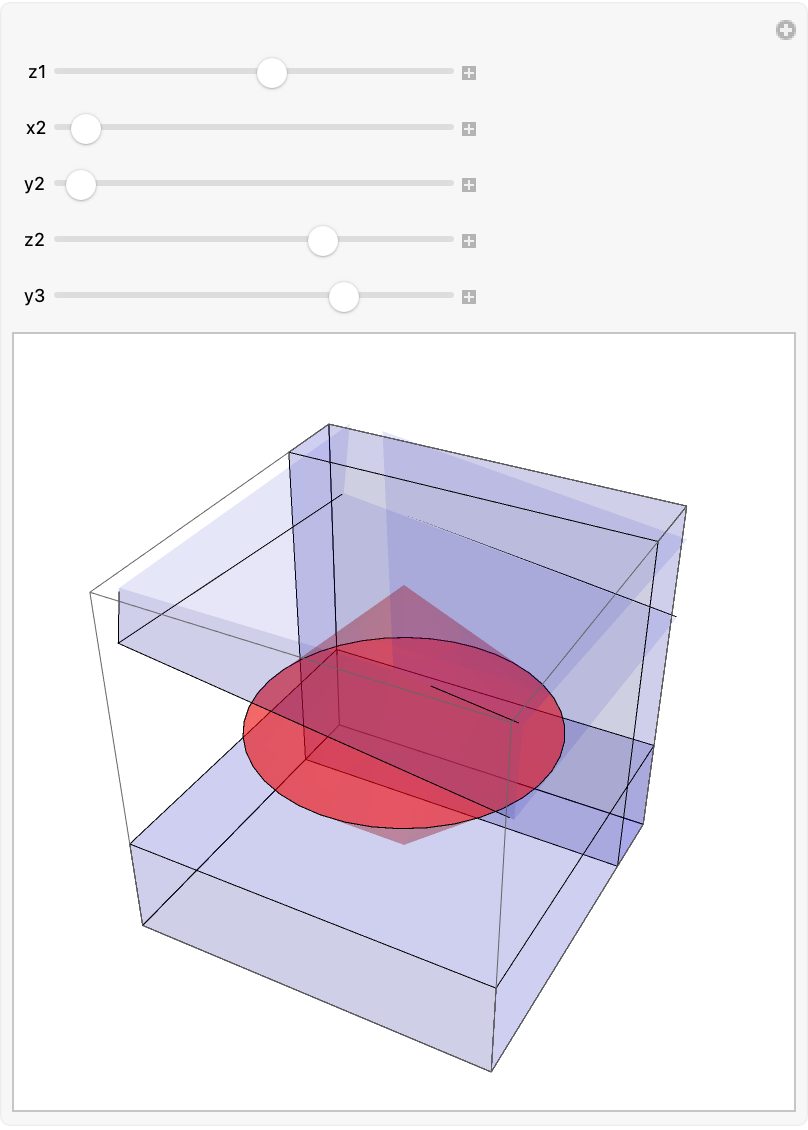
The plane definitions are copied to the clipboard; let us paste them here to use subsequently:

Object definition

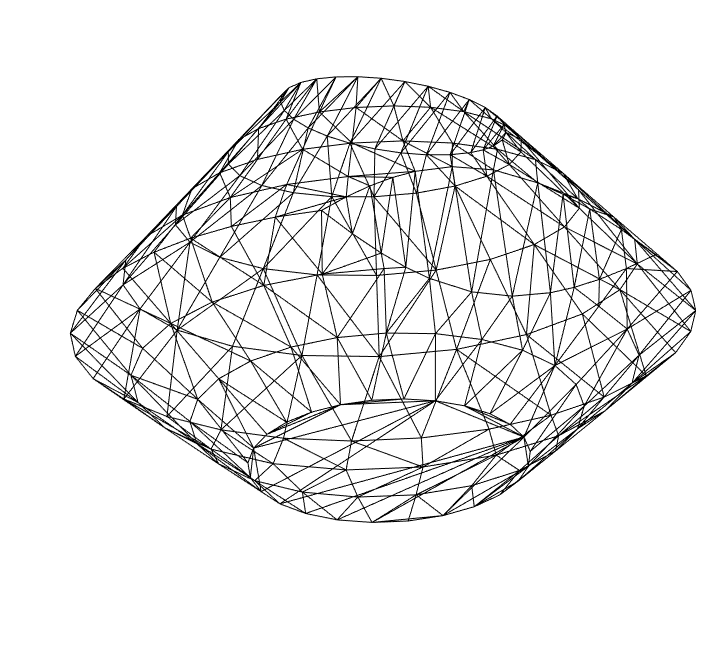
Now we define the basic object with OpenCascadeLink:

Needs["OpenCascadeLink`"]

object = Module[
    {b = OpenCascadeShapeUnion @@ OpenCascadeShape /@ bicone[4], 
     cubes = OpenCascadeShape /@ def["cubes"]}, 
    cubes[[2]] = OpenCascadeShapeTransformation[cubes[[2]], def["rotation"]]; 
    OpenCascadeShapeDifference[
     b, 
     Fold[OpenCascadeShapeUnion, cubes]]] 
 
OpenCascadeShapeSurfaceMeshToBoundaryMesh[object]["Wireframe"]

(*OpenCascadeShapeExpression[10]*)

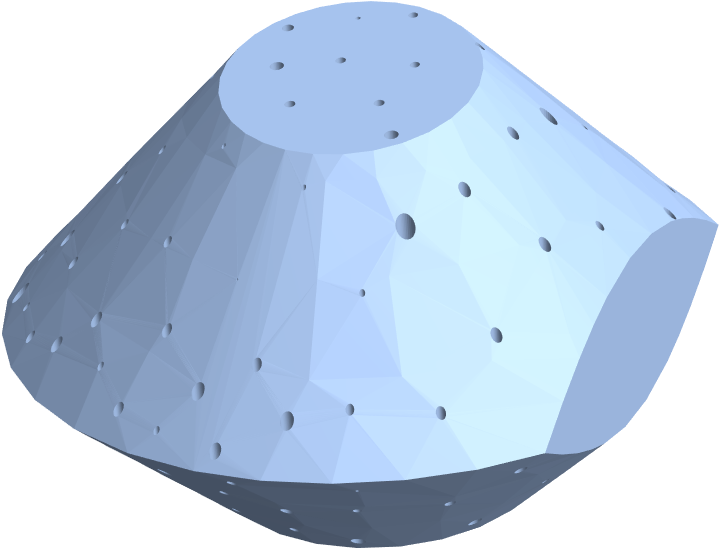
Now perform the punching operation as defined in the previous post in this series. We will not bother with shelling this in OpenCascade, as is is better to do this in the slicer anyway:

(*unmodified from the last post*)
  punch[direction_ : 1, count_ : 86] := With[
    {boundary = Disk[{0, 0}, 4]}, 
    With[
     {centers = ResourceFunction["LloydAlgorithm"][
        RandomPoint[boundary, count], boundary, 2], 
      radii = RandomVariate[NormalDistribution[0.05, 0.02], count]}, 
     MapThread[
      If[#2 > 0, 
        Cylinder[ {Append[0]@#1, Append[4*direction]@#1}, #2], 
        Nothing] &, 
      {centers, radii}]]]

punched = With[
    {punches = OpenCascadeShape /@ Flatten[{punch[1], punch[-1]}]}, 
    OpenCascadeShapeDifference[object, 
     Fold[OpenCascadeShapeUnion, punches] 
    ]] 
 
OpenCascadeShapeExport["foo.stl", punched];
Import["foo.stl"]

(*OpenCascadeShapeExpression[694]*)

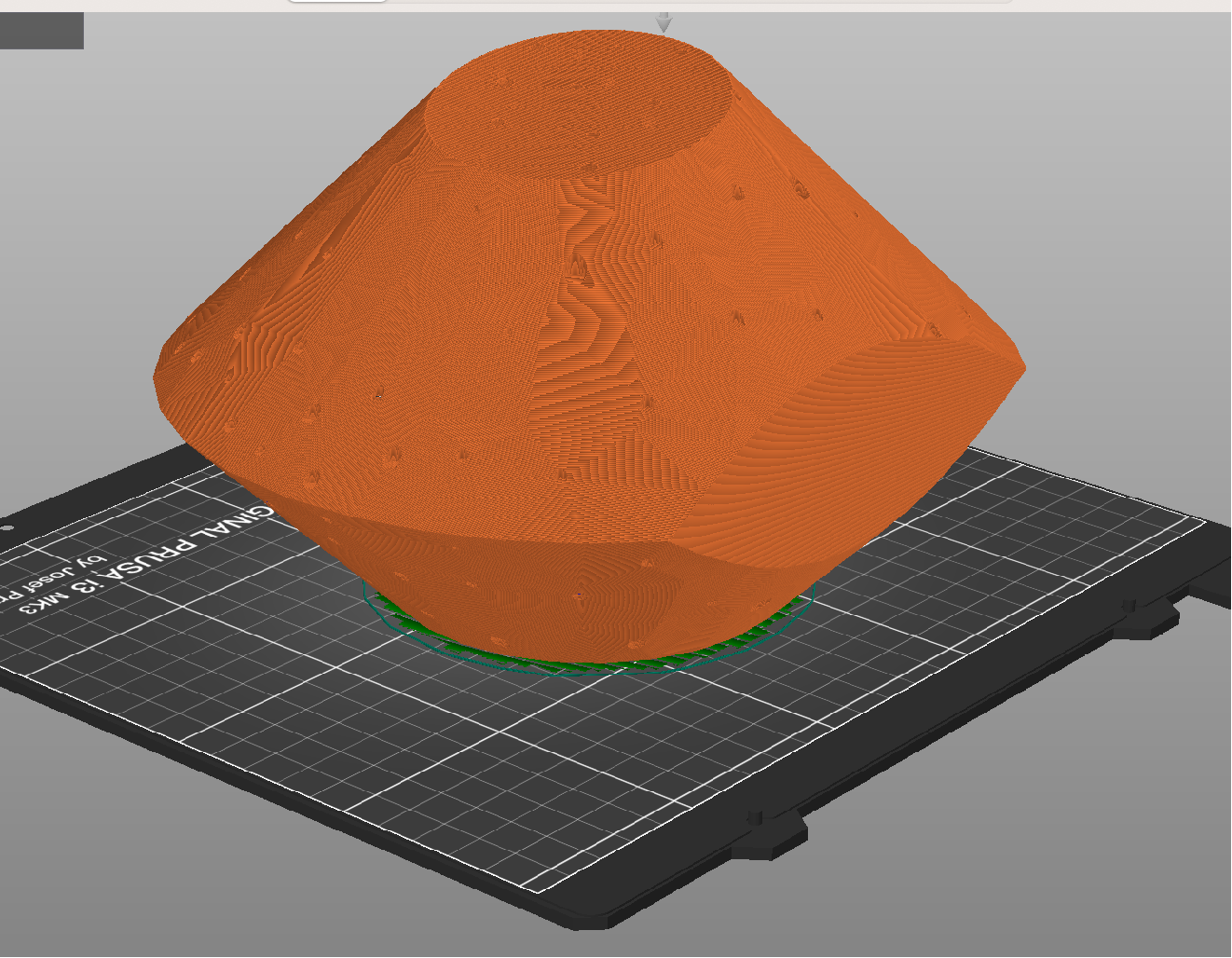
Pull it up in PrusaSlicer: Vase mode setting, no top or bottom layers, but add a 1 layer raft. 6h41m print at 0.1mm layer height, ~30g of filament required; no apparent support errors. Previous post contains information on suitable filaments for printing, etc.

ToJekyll["Computational Sculpture: After Karen Bexfield, part 2", "art opencascade 3dprinting mathematica santafe sculpture"]