Running WebMO Quantum Chemistry Calculations in Mathematica
[chemistry teaching mathematica WebMO is a web-based interface to computational chemistry software used by many schools for teaching and research purposes. The WebMO Enterprise edition supports a REST API allowing you to access job information and create new jobs, which we can use to run quantum chemistry calculations with Mathematica…
Prelude: Storing Login Information
It is useful to store the information about the URL and username/password information in a way that facilitates their later use. Mathematica provides some convenient ways to do this: PersistentSymbol stores values that can be drawn later. SystemCredential provides a secure storage using the operating system user keychain.
For the purposes of this tutorial, we will use the public WebMO demonstration server, and associated login information (which is not secret):
PersistentSymbol["WebMO_URL", "Local"] = "https://www.webmo.net/demoserver/cgi-bin/webmo/rest.cgi/";
SystemCredential["WebMO"] = SystemCredentialData[
<|"username" -> "guest", "password" -> "guest"|>,
"password"]
Notice how the DisplayForm keeps our password secret:
SystemCredential["WebMO"]

But all of the information is present in the InputForm:
InputForm[%]
SystemCredentialData[<|"username" -> "guest", "password" -> "guest"|>, "password"]
We can always pull out the information by taking the first entry:
First@ SystemCredential["WebMO"]
(* <| "username" -> "guest", "password" -> "guest" |> *)
Of course, in real life, you would use the URL, username, and password of your own server and not publish it on your blog…
Prelude: Constructing URLs
The various REST API functionalities are accessed by different URLs (or more pedantically, URIs). If you are a chemist who is unfamiliar with the ideas of REST, there is a nice introduction in the Libretext cheminformatics course. tl;dr–we just need to append some additional information to the base URL, and we can do this in multiple ways. Perhaps the simplest is just to use a string concatenation:
With[
{url = PersistentSymbol["WebMO_URL"] <> "status"},
URLExecute[url] ]
(*{"url_cgi" -> "https://www.webmo.net/demoserver/cgi-bin/webmo", "jobs" -> 1755775, "timestamp" -> "9/30/2025 18:21", "url_html" -> "https://www.webmo.net/demoserver/webmo", "version" -> "25.1.002e"}*)
And we see an example output here, which is returned as a list-of-rules data structure!
But it is probably better to use URLBuild to do this, which will take care of escaping characters etc.:
URLExecute@
URLBuild[{PersistentSymbol["WebMO_URL"], "status"}]
(* {"timestamp" -> "9/30/2025 18:21",
"version" -> "25.1.002e",
"url_html" -> "https://www.webmo.net/demoserver/webmo",
"url_cgi" -> "https://www.webmo.net/demoserver/cgi-bin/webmo",
"jobs" -> 1755775} *)
Obtaining a session token
Aside from a status request, other operations involving calculation job information require us to log in to the server and obtain an authentication token. This is accomplished through the sessions REST API endpoint. It is slightly more complicated, as it requires a POST operation (instead of the default GET), so we first construct the HTTPRequest with this information:
auth = URLExecute@ HTTPRequest[
URLBuild[{PersistentSymbol["WebMO_URL"], "sessions"}],
<|"Method" -> "POST", "Body" -> First@ SystemCredential["WebMO"]|> ]
(*{"username" -> "guest", "token" -> "QfZaqJyHLX."}*)
When we request job information, we will provide this authorization token information as an additional argument:
URLExecute[
URLBuild[{PersistentSymbol["WebMO_URL"], "jobs", ToString[1755764]}],
auth]
(* {"properties" -> {"jobDate" -> "9/30/2025 18:17",
"jobStatus" -> "complete", "jobGroup" -> "webmo",
"pid" -> 2070200, "cpu_time" -> 0.02, "failureCode" -> 0,
"folderID" -> 0, "jobUser" -> "guest", "server" -> "webmo.net",
"jobDescription" -> "Geometry Optimization",
"checkpointFile" -> 0, "jobNumber" -> 1755764,
"jobName" -> "H2Se", "jobEngine" -> "mopac"}, "jobNumber" -> 1755764} *)
The authorization token has a finite lifetime and will expire.
Accessing information about a completed job
To simplify the process, define a function to collect the jobID number, authorization token information, and an optional property string. This is just a generalization of the code above into a function. As the jobID is numerical, we shall be sure to convert it ToString before building the URL:
jobs[jobID_, auth_, property_ : Nothing] := URLExecute[
URLBuild[{PersistentSymbol["WebMO_URL"], "jobs", ToString[jobID], property}],
auth ]
(*demo*)
jobs[1755764, auth]
(* {"properties" -> {"jobDescription" -> "Geometry Optimization",
"cpu_time" -> 0.02, "checkpointFile" -> 0, "jobNumber" -> 1755764,
"jobEngine" -> "mopac", "failureCode" -> 0, "jobUser" -> "guest",
"server" -> "webmo.net", "folderID" -> 0, "jobDate" -> "9/30/2025 18:17",
"jobStatus" -> "complete", "jobName" -> "H2Se", "jobGroup" -> "webmo",
"pid" -> 2070200}, "jobNumber" -> 1755764} *)
As described in the WebMO REST API documentation, the geometry suboption returns the final geometry information about the job:
geom = jobs[1755764, auth, "geometry"]
(* {"zmatrix" -> "1 0 0 0 2 1 0 0 3 1 2 0 ",
"jobNumber" -> 1755764,
"xyz" -> "Se -0.131093435 -0.042780120 -0.010000000H 1.331436372 0.103746597 -0.010000000H -0.368371382 1.407792591 -0.010000000", "charges" -> "0 3 0 0 0 0 0 0 0 ",
"connections" -> "1 2 1 1 3 1 "} *)
It is straightforward to parse the Cartesian coordinates block and then import as a Molecule for modification and display in Mathematica:
ImportString[#, "XYZ"]&@ Lookup["xyz"]@ geom
MoleculePlot3D[%]

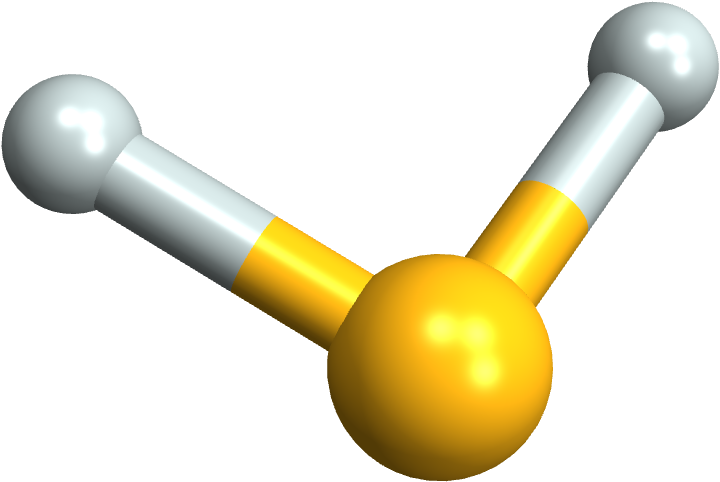
The results option returns a QC-JSON schema description, a semi-standard way of interacting with quantum chemistry packages:
jobs[1755764, auth, "results"]
(* {"symbols" -> {"Se", "H", "H"},
"molecular_charge" -> 0, "comment" -> "H2Se; Geometry Optimization",
"connectivity" -> { {1, 2, 1}, {1, 3, 1}},
"properties" -> {"cpu_time" -> {"value" -> 0.02, "units" -> "sec"},
"dipole_moment" -> {-0.82, -1.069, 0},
"scf_dipole_moment" -> {-0.82, -1.069, 0},
"partial_charges" -> {"mulliken" -> {0.036786, -0.018393, -0.018393}},
"method" -> "PM3", "pm3_energy" -> {"units" -> "kcal/mol", "value" -> 22.7248},
"route" -> "PM3 BONDS CHARGE=0 SINGLET XYZ PRNT=2 PRTXYZ FLEPO PRECISE GNORM=0.0",
"method_energy_name" -> "PM3", "symmetry" -> "C2v",
"geometry_sequence" -> {"energies" -> {22.8913, 22.7644, 22.7258, 22.7248}, "units" -> "kcal/mol", "geometries" -> { {-0.11, -0.0329, -0.01, 1.3251, 0.0886, -0.01, -0.3833, 1.4006, -0.01}, {-0.121, -0.035, -0.01, 1.3411, 0.0937, -0.01, -0.3776, 1.4011, -0.01}, {-0.1304, -0.0439, -0.01, 1.3322, 0.1037, -0.01, -0.369, 1.4094, -0.01}, {-0.1309, -0.0428, -0.01, 1.3318, 0.1036, -0.01, -0.3686, 1.4079, -0.01}}}},
"provenance" -> {"creator" -> "Mopac"},
"geometry" -> {-0.131093, -0.0427801, -0.01, 1.33144, 0.103747, -0.01, -0.368371, 1.40779, -0.01}, "schema_name" -> "QC_JSON", "success" -> True,
"molecular_multiplicity" -> 0, "schema_version" -> 0}*)
Creating new jobs
To create your own quantum chemistry calculation job you will need to know something about the underlying quantum chemistry software engine that is available on your server, and its input format. This is beyond the scope of the current tutorial, so I will just show a simple Gaussian16-style input for the hydrogen molecule. Begin by creating a list of rules that describe the name, engine, and input file contents (the key names are important, as are the new-lines in the inputFile definition):
jobInput = {
"jobName" -> "H2 optimization",
"engine" -> "gaussian",
"inputFile" -> "#N HF/STO-3G OPT
H2 demo
0 1
H 0.0 0.0 0.0
H 0.0 0.0 1.0
"};
Now, we just send this to the jobs REST endpoint. The difference here is that we must do this via a POST to send the input values, and that also needs to include our authentication token information. We could define a new function for this, but for the sake of moving the tutorial along, we will not…
newJob = URLExecute@ HTTPRequest[
URLBuild[{PersistentSymbol["WebMO_URL"], "jobs"}],
<|"Method" -> "POST", "Body" -> Join[jobInput, auth]|> ]
(* {"jobNumber" -> 1755864} *)
Check on the job status:
jobs[1755864, auth]
(* {"jobNumber" -> 1755864,
"properties" -> {"jobUser" -> "guest", "jobNumber" -> 1755864,
"folderID" -> 0, "server" -> "webmo.net", "jobEngine" -> "gaussian",
"checkpointFile" -> 0, "jobGroup" -> "webmo", "failureCode" -> 0,
"jobDate" -> "9/30/2025 18:55", "pid" -> 2075525, "jobStatus" -> "complete",
"cpu_time" -> 1.9, "jobDescription" -> "Execute", "jobName" -> "H2 optimization"}} *)
Check on the results:
results = jobs[1755864, auth, "results"]
(* {"symbols" -> {"H", "H"}, "geometry" -> {0, 0, 0.356115, 0, 0, -0.356115},
"properties" -> {"basis" -> "STO-3G", "cpu_time" -> {"value" -> 1.9, "units" -> "sec"},
"quote" -> " SATCHEL PAIGE'S GUIDE TO LONGEVITY 1. AVOID FRIED MEATS, WHICH ANGRY UP THE BLOOD. 2. IF YOUR STOMACH DISPUTES YOU, LIE DOWN AND PACIFY IT WITH COOL THOUGHTS. 3. KEEP THE JUICES FLOWING BY JANGLING AROUND GENTLY AS YOU MOVE. 4. GO VERY LIGHT ON THE VICES, SUCH AS CARRYING ON IN SOCIETY. THE SOCIAL RUMBLE AIN'T RESTFUL. 5. AVOID RUNNING AT ALL TIMES. 6. DON'T LOOK BACK. SOMETHING MAY BE GAINING ON YOU.",
"method_energy_name" -> "HF", "scf_dipole_moment" -> {0, 0, 0},
"dipole_moment" -> {0, 0, 0}, "partial_charges" -> {"mulliken" -> {0, 0}},
"rotational_constants" -> {0, 1977.07, 1977.07},
"symmetry" -> "D*H",
"geometry_sequence" -> {"geometries" -> { {0, 0, 0.5, 0, 0, -0.5}, {0, 0, 0.420623, 0, 0, -0.420623}, {0, 0, 0.348515, 0, 0, -0.348515}, {0, 0, 0.356256, 0, 0, -0.356256}, {0, 0, 0.356115, 0, 0, -0.356115}}, "units" -> "Hartree", "energies" -> {-1.06611, -1.10415, -1.11726, -1.11751, -1.11751}}, "rhf_energy" -> {"value" -> -1.11751, "units" -> "Hartree"},
"method" -> "HF", "stoichiometry" -> "H2", "route" -> " #N HF/STO-3G OPT"},
"schema_name" -> "QC_JSON", "success" -> True, "molecular_multiplicity" -> 0,
"connectivity" -> { {1, 2, 1}},"comment" -> "H2 optimization; Execute",
"molecular_charge" -> 0, "schema_version" -> 0, "provenance" -> {"creator" -> "Gaussian"}} *)
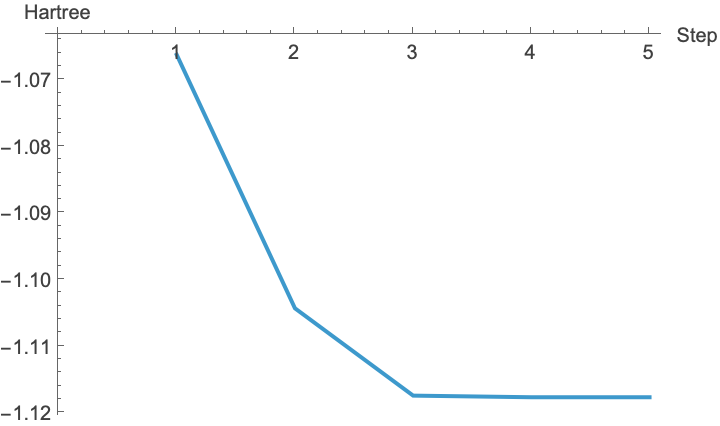
We can pull information out of the results and bring it into Mathematica, as demonstrated earlier for the geometry, etc. Different types of calculations will have different output information. In this case, we performed a geometry optimization, so the results include information about the energy at each step along the geometry optimization process; let us extract this and plot the result:
ListLinePlot[
Query["properties", "geometry_sequence", "energies"]@ results,
AxesLabel -> {"Step", Query["properties", "geometry_sequence", "units"]@ results} ]
ToJekyll["Running WebMO Quantum Chemistry Calculations in Mathematica", "chemistry teaching mathematica"]