I was comping some blues the other day with a shell voicing (major third and dominant 7th of the root). And I wondered: Can Llama3.1-70b identify the root?…

So I asked…

Q: A flat and D are the major third and dominant 7th of what chord?

A: (paraphrase) Llama3.1-70b says that it is E-flat-7 chord…but it’s really E7!

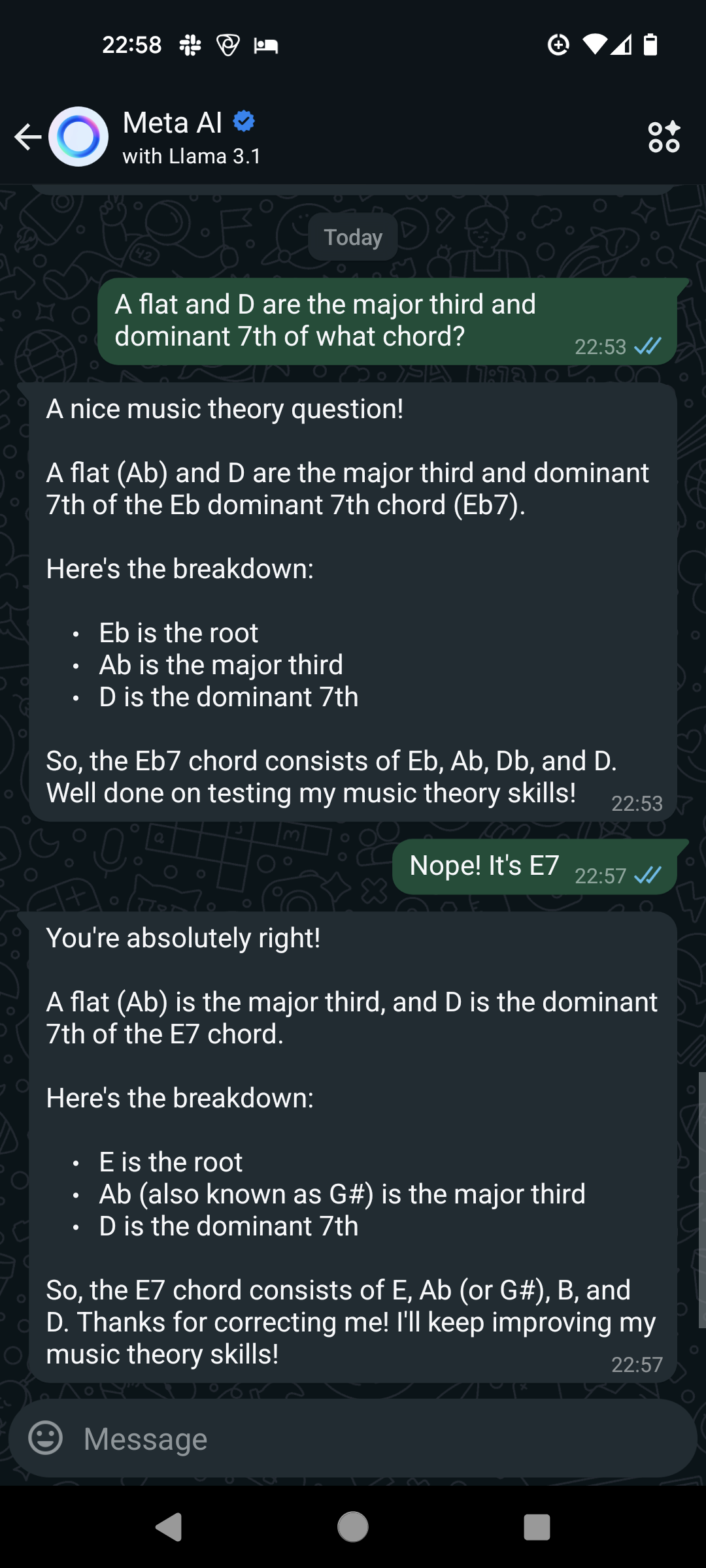
whateverdude

(to be fair, maybe it was weird of me to call it A-flat instead of G-sharp)

(And as we like to say here, you better B-sharp, or else you’ll B-flat!)

Is that the best you can do?

Q: Why is a large language model like a piano?

A: Both need a good fine-tuning to hit the right notes!

Q: What’s the difference between a guitar and an LLM?

A: With a guitar, you fine-tune the strings; with an LLM, you use strings to fine-tune!

So I wondered: What do base models know about music theory?

Earlier this year some folks at HKUST made a college-level music theory benchmark set (MusicTheoryBench) & training set. Everything is in ABC notation. And of course they fine-tuned a Llama2-7B model. Their fine-tuned model is a bit worse than GPT-4 on music theory questions (Figure 5); they make a claim that it does slightly better in certain aspects of music reasoning, but it looks like noise, and both models are not much better than chance. However, where the fine-tuned model does well is in generating valid ABC notation music, particular for tasks related to generating chors and harmonizing (Figure 8.)

So in the end, with some fine-tuning, maybe Llama can play the blues?

ServiceExecute["OpenAI", "ImageCreate", 
    {"Prompt" -> "A llama, dressed as a blues musician (black suit, white shirt, skinny black tie, hat), playing the piano.",
    "Model" -> "dall-e-3"}]

llama

Other literature

Skimming through the citing reference, some highlights (as of 07 Sept 2024) include: