In a previous post, we discussed the use of LLMTool, to provide a way for remote LLMs to execute code on your local Wolfram kernel. A natural place to use this is in performing numerical calculations–mathematical calculations are a well-known weakness of LLMs. We can solve this by having the LLM write the proposed calculation as a string, and then call a tool that Evaluate-s it on the local kernel. But Evaluate-ing any arbitrary string provided is a recipe for trouble–a malicious actor would be able to use this to perform arbitrary calculations, such as deleting files, etc. (This is not unique to Mathematica: we all know python eval is dangerous, and the modern best practice is to sandbox an entire python install.) Interpreter provides a safe and easy way to provide LLMs with the ability to perform only numerical calculations with Mathematica…

Use Interpreter to perform safe calculations

(a riff off a recent stackexchange post) Interpreter lets you parse input strings into wide range of object types. For our goal of allowing arbitrary numerical calculations, ComputedNumber **seems like the right choice, but other possibilities include MathExpression (to perform equation solving) or ComputedQuantity (to perform unit calculations).

Simple arithmetic expressions work fine:

Interpreter["ComputedNumber"]["1+1"]

(*2*)

But we return a Failure if the input is non-numerical:

Interpreter["ComputedNumber"]["1+Quit[]"]

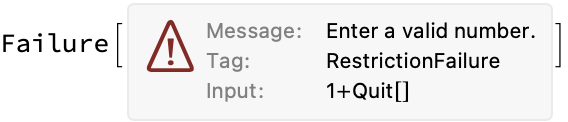
199f6u5lju4dy

However, we are still allowed to use any built-in function that performs a numerical computation:

Interpreter["ComputedNumber"]["1+Sin[3.2 Pi]"]

(*0.412215*)

ComputedNumber has access to expressions outside of the input scope, so long as they compute a number:

a = {1, 2, 3};
Interpreter["ComputedNumber"]["1+a[[2]]+a[[3]]"]

(*6*)

The interpreter is smart enough to distinguish between indefinite integrals which return a symbolic result:

Interpreter["ComputedNumber"]["Integrate[x, {x}]"]

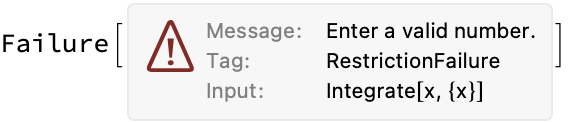
0dxszrbqe9zaz

As opposed to definite integrals which return a numerical result:

Interpreter["ComputedNumber"]["Integrate[x, {x,0,1}]"]

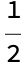
1mt5g4rpp664w

In conclusion: This is exactly what we want.

However: A possible limitation is that a malicious code could still, in principle, crash our kernel by requesting some difficult calculation (e.g., trying to do root solving on a high order polynomial.) Howeer, this can be limited by wrapping the evaluation in a TimeConstrained and/or MemoryConstrained functions to impose a hard limit on the computational resources for the task.

Implement the LLMTool

In a previous post, we showed how to define an LLMTool. Let’s do it again, but this time evaluate arbitrary numerical expressions with our safe interpretation. Conveniently, we can impose the Interpreter type on the input variables by providing a rule in the second argument:

calculate = LLMTool[
    {"calculate", (*name*)
     "e.g. calculate: 1+1\ne.g. calculate: 1+Sin[3.2 Pi]\nRuns a calculation and returns a number - uses Wolfram language as determined by  Interpreter[\"ComputedNumber\"]."}, (*description*)
    "expression" -> "ComputedNumber", (*interpretation is performed directly on input*)
    ToString[#expression] &]; (*convert back to string to return to LLM*)

Without the tool, the results are poor (using gpt-4-1106-preview by default):

LLMSynthesize["What is 1+ Sin[7.8/Pi]?"]

(*"1 + sin[7.8/Pi] is approximately equal to 1.01228."*)

With the tool, the result is correct (of course, because it uses the tool)

LLMSynthesize["What is 1+ Sin[7.8/Pi]?", 
  LLMEvaluator -> <|"Tools" -> calculate|>]

(*"The result of the expression 1+Sin[7.8/Pi] is approximately 1.61215."*)

ToJekyll["Accurate and safe LLM numerical calculations using Interpreter and LLMTool", 
  "llm gpt4 mathematica"]

Parerga and paralipomena