While reading Mandelbrot’s Fractal Geometry of Nature, I wondered about what would be the sound of a square wave defined by the intervals of each iteration of a Cantor set. One can imagine the first iteration is just a square wave (with a non-50% duty cycle), and that other iterations will potentially be waves with higher frequency. (This would define a niche genre of 1-bit music .) What will it sound like?…

CantorSquareWave[freq_, n_, t_] := With[
    {cantorSetLimits = Partition[#, 2]& @ Flatten @ MeshCoordinates @ CantorMesh[n]}, 
    Boole @ Between[ Mod[freq*t, 1], cantorSetLimits]] 
 
ListAnimate[
  Plot[CantorSquareWave[3, #, t], {t, 0, 1}] & /@ Range[10]]

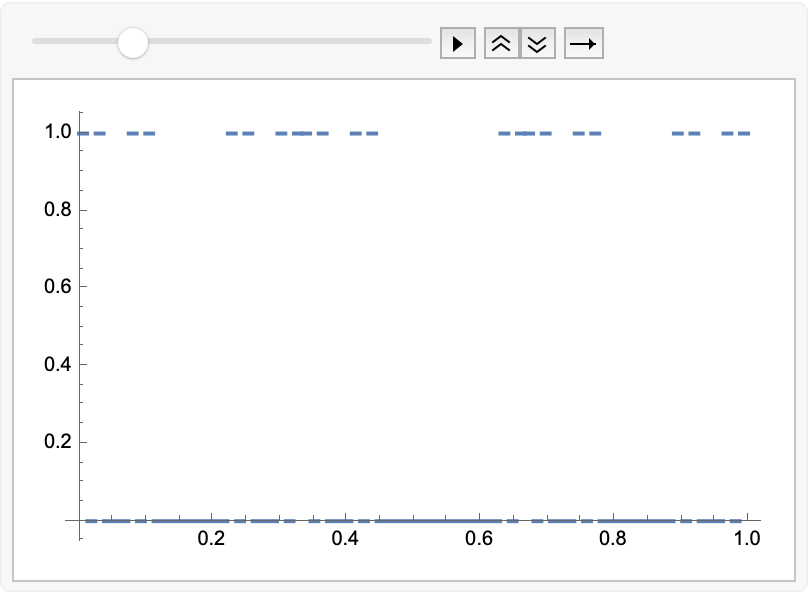
1ombpmnxzvkh7

It is straightforward to turn this into a sound, using a 256 Hz base frequency:

Play[CantorSquareWave[256, 1, t], {t, 0, 1}]

0bumz4laq5q4y

Now, sonify a progression of iterations (one second each). I increased the sampling rate to better capture the high frequency variations.

result = Sound@ParallelMap[
     Play[ (CantorSquareWave[256, #, t]), {t, 0, 1}, SampleRate -> 22000] &, 
     Range[10]] 
 
Export["cantorset.mp3", result]

0ditpuu99382j

(*"cantorset.mp3"*)

You can download this MP3 file from this link. (Generating this gets very slow for large iteration values in the Cantor set.)

What surprised me is how you at first hear a doubling of the frequency (moving up an octave), but then this stops as the duty cycle gets too low. The effect is also not particularly pleasant, so I suppose that is why it is not used more often.

Surprisingly, I could not find other people who had considered this experiment. However, some related experiments I found while waiting for the computation to finish include:

  • David Madore, The Sound of a Cantor Set – “The sound signal whose Fourier transform equals the uniform distribution on the standard Cantor triadic set placed between 1056Hz (just/natural C6) and 3168Hz (just/natural G7). The graph shows the spectrum in question.”

  • Matthew McGonagle, Making an Audio .wav File of Cantor Tones – where each tone is mapped to one of the iterations in a Cantor Set, s that they have different rhythms. (Could be a fun future exploration…)

  • CantorDust fractal sonification tool

  • Almeida et al Low-frequency broadband sound absorption based on Cantor fractal porosity JAP 2023.–“Proposals for new absorber designs for broadband sound absorption are of great interest due to their wide applicability in sound energy control. In this sense, the behavior of an acoustic absorber composed of a panel with slit-type perforations based on Cantor’s fractal is presented. The analytical model for the fractal porosity of the absorber as a function of the initial geometric parameters, the number of iterations, and the fractal dimension was established. The behavior of broadband sound absorption was evaluated theoretically, numerically, and experimentally, in which the predominant total thermal-viscous dissipation in the region of perforations increases as the fractal porosity of the absorber decreases. Furthermore, an experimental broadband sound absorption of 692 Hz (from 382 to 1074 Hz) with a peak amplitude greater than 80% is obtained with the proposed structure presenting a sub-wavelength scale, i.e., [NoBreak]. Finally, this work contributes to the understanding of the use of Cantor’s fractal porosity in the proposal of new absorbers that allow broadband sound absorption at low frequency.”

ToJekyll["Sound of a Cantor Set Square Wave", "fractal audio synth 8bit"]