Retrieval Augmented Generation

User5601 asks: How can I implement retrieval augmented generation (RAG) using the new LLM functionality in Mathematica 13.3? There are many desirable reasons for using RAG: It allows you to provide your own domain-specific information and to make citations to sources. Let’s implement a RAG that can answer questions using the Catechism of the Catholic Church…

The essential process is:

1. Define a collection of texts and pre-process them so that they are a suitable length for the LLM context window

2. Use the LLM to generate embedding vectors for each text item and store it for later use.

3. When a new question is posed, generate its embedding vector and then find the Nearest vector in the collection of texts computed in #2; use this to retrieve relevant texts

4. Send the question and the retrieved text to an LLM to generate the response

Pre-processing

As an example, we will use the English language version of the Catechism of the Catholic Church. In addition to being good for your soul, it is also a large document that comes with a built-in segmentation into smaller pieces, is mostly plain-text HTML with minimal formatting, and is available for free online.

We’ll retrieve the index page, and then use the links in the page to retrieve the remainder of the content; this example is small enough that we can store everything in memory:

sectionLinks = With[
    {url = "https://www.vatican.va/archive/ENG0015/_INDEX.HTM"}, 
    Drop[#, 10] &@Import[url, "Hyperlinks"]]; (*first 10 links are navigation tools*)

texts = Import[#, "Plaintext"] & /@ sectionLinks;

Some statistics about the documents:

Length[texts] (*how many documents do we have? *)

(*374*)

wordCounts = WordCount /@ texts;
MinMax[%](*how long are they?*)

(*{72, 6670}*)

GPT-style models have a limit on the number of input tokens. A rule of thumb is that a token is roughly 0.75 words (or a word is on average 1/0.75 = 1.3 tokens). For GPT-3.5, the maximum input content lengths is 8191 tokens, so we’ll want to make sure that the texts that we provide are less than this, otherwise we will get an error when we generate the embeddings, which will look something like this:

Tools like tiktoken can be used to count the tokens in an input. To get a rough estimate, we’ll use t for gpt2, we’ll use the GPTTokenizer resource function :

tokenEncoder = ResourceFunction["GPTTokenizer"][];
tokenCounts = Length /@ tokenEncoder /@ texts;
MinMax[%]
Histogram[%%]

(*{123, 9435}*)

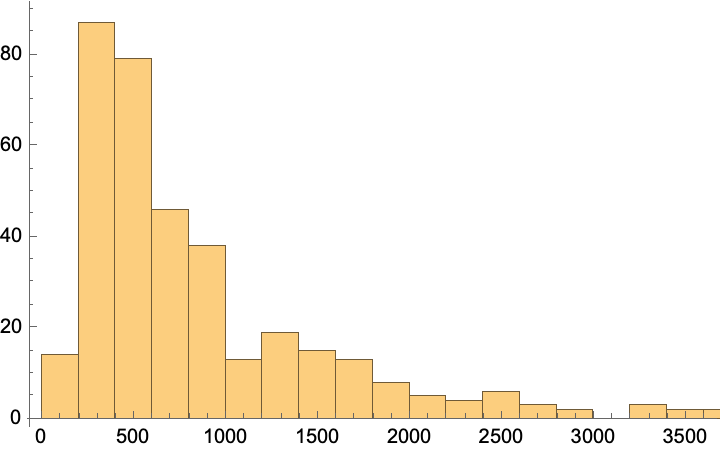
Only a few of the texts are long ones containing more than 4000 tokens.

Sort@Select[GreaterThan[4000]]@tokenCounts

(*{4033, 4128, 4171, 4215, 4461, 4714, 4881, 5175, 5496, 6737, 8499, 9404, 9435}*)

I suppose we may as well make the comparison:

ListPlot[
  Transpose[{wordCounts, tokenCounts}], 
  PlotRange -> All]

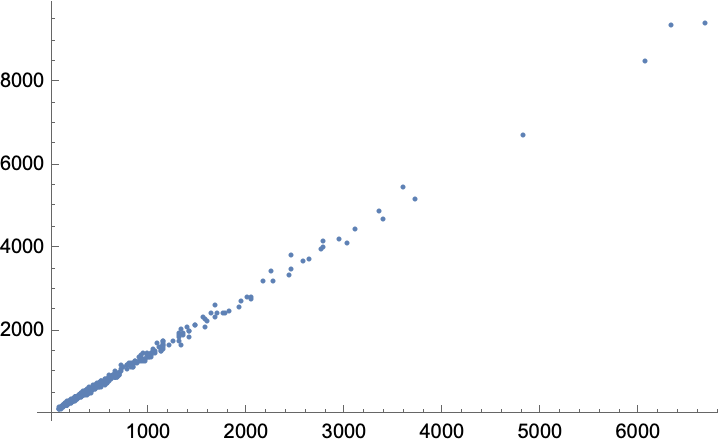
model = LinearModelFit[Transpose[{wordCounts, tokenCounts}], {1, x}, x]

Based on this, let’s set 4000 words as a reasonable place to divide the text

Clear[splitWords] 
 
notTooLong[str_String] := WordCount[str] < 4000 
 
splitWords[str_?notTooLong] := str 
 
splitWords[str_] := Module[{words, half}, 
   words = StringSplit[str]; 
   half = Ceiling[Length[words]/2]; 
   {StringJoin[Take[words, half]], StringJoin[Drop[words, half]]}]

We’ll ultimately find 4 of these and just chop them in half. Of course, in production, you might do something smarter.

Length[(shorterTexts = splitWords /@ texts // Flatten)]

(*378*)

Compute Embedding Vectors

Next, compute the embedding vectors for each of these texts using the LLM model of your choice:

• To do this offline (with short texts) you can do this with GPT2, the section on Sentence Analogies in the Wolfram Neural Net Repository shows how to get the sentence embeddings

• Using OpenAI GPT 3.5/4 embeddings one can use Christopher Wolfram’s OpenAILink paclet (oddly, the LLM support built into Mathematica 13.3 doesn’t include a function for embedding calculations)

• to do this with Google’s PaLM you can use the Anton Atonov’s PaLMLink paclet

We’ll do this using the OpenAI embeddings, so we must first setup the OpenAI Link paclet:

PacletInstall["ChristopherWolfram/OpenAILink"]

Needs["ChristopherWolfram`OpenAILink`"]

embeddings = OpenAIEmbedding /@ shorterTexts;

Note: This will cost about $0.05 USD and it takes a minute to make all the API calls sequentially. So let’s save these for later reuse:

SetDirectory@NotebookDirectory[];
data = Dataset[<|"text" -> shorterTexts, "vector" -> embeddings|>];
Save["catechism_embeddings.wl", data]

Now we’ll also use these to create a NearestFunction that can be applied to future data. It is standard practice to use the CosineDistance when comparing embedding vectors.

lookupFn = Nearest[embeddings -> shorterTexts, DistanceFunction -> CosineDistance]

If you were scaling this up, you would probably want to store the texts in a database and have the Nearest function just return keys that would be used for lookup. Commercial offerings like pinecone.io can handle this for you.

Vector Retrieval

Next we take a question, generate its embedding vector and then use it to find the nearest relevant text. Let’s try it:

question = "What must I do to have eternal life?";
questionEmbedding = OpenAIEmbedding[question];
closestText = lookupFn[questionEmbedding]

(*{"HelpCatechism of the Catholic ChurchIntraText - TextPART THREE: LIFE IN CHRISTSECTION TWO THE TEN COMMANDMENTSIN BRIEF Previous - NextIN BRIEF  2075 \"What good deed must I do, to have eternal life?\" - \"If you would enter into life, keep the commandments\" (Mt 19:16-17).  2076 By his life and by his preaching Jesus attested to the permanent validity of the Decalogue. 2077 The  gift of the Decalogue is bestowed from within the covenant concluded by God with his people. God's  commandments take on their true meaning in and through this covenant.  2078 In fidelity to Scripture and in conformity with Jesus' example, the tradition of the Church has always  acknowledged the primordial importance and significance of the Decalogue.  2079 The Decalogue forms an organic unity in which each \"word\" or \"commandment\" refers to all the others  taken together. To transgress one commandment is to infringe the whole Law (cf Jas 2:10-11).  2080 The Decalogue contains a privileged expression of the natural law. It is made known to us by divine  revelation and by human reason.  2081 The Ten Commandments, in their fundamental content, state grave obligations. However, obedience  to these precepts also implies obligations in matter which is, in itself, light.  2082 What God commands he makes possible by his grace.  Previous - NextCopyright (c) Libreria Editrice Vaticana"}*)

You’ll notice that the text retrieved seems relevant but includes line numbers and other formatting information.

Answer the query using the retrieved text

Finally, we provide our input question and the retrieved the closestText to the LLM; Here we will use the built-in LLMSynthesize function, and a fairly minimal prompt.

LLMSynthesize[
  StringJoin[
   "Answer this question: ", question, 
   "\n Based on the following context:", closestText]]

(*"According to the Catechism of the Catholic Church, to have eternal life, one must keep the commandments. Jesus stated, \"If you would enter into life, keep the commandments\" (Mt 19:16-17). The Decalogue, which includes the Ten Commandments, holds a privileged expression of the natural law, and obedience to these precepts implies obligations in both grave and light matters. It is also important to note that God's grace makes it possible to fulfill His commands."*)

As you can see, this has reworded and paraphrased the retrieved text to answer the question. Because we know what text was used, we could also provide a citation, if desired. Ite, missa est.

2023.08.22_llm_qa_demo.nb

Parerga and Paralipomena

• HYDE is a strategy whereby you ask your generative model to create possible answers to the question (it doesn’t matter whether they are right or wrong), and then you use the embeddings of those generated sentences to perform the retrieval. The idea here is that the the embedding of the question and the embedding of an answer are likely to be different, and you will be more likely to retrieve a relevant answer text if you compare it to other answer-y type values
• The new GPTTokenizer resource function facilitates token counting
• (18 Apr 2024) OpenAI now supports FileSearch which will do the file parsing, chunking, embedding, and vector lookup for you…
• (01 Aug 2024) The new Mathematica 14.1 has built in semantic search and vector database capabilities