Some notes on Benoit Mandelbrot & Richard Hudson, The (Mis)behavior of Markets: A Fractal View of Financial Turbulence (2004). Premise: The (geometric) Brownian motion model of asset prices, and the house built upon its Gaussian foundation (i.e., Bachelier, Markowitz efficient portfolios, Sharpe’s Capital Asset Pricing Model, Black-Scholes) fails to capture the extreme variations present in real-data. Power law distributions, fractional Brownian motion (which has postive or negative time-correlations) and multi-fractal regime changes better capture observed variations…

Notes

  • pp. 20+ Five rules
    1. Markets are risky
    2. Trouble runs in streaks
    3. Markets have a personality
    4. Markest mislead
    5. Market time is relative
  • p. 184: corrolograms of tree-ring data
  • p. 191: estimate H for different asset types (Taqqui)
  • p. 208: Two types of variability: Noah (big changes can happen, governed by power law, with parameter \alpha) & Joseph (persistent motion/time correlations: described by fractional brownian motion with parameter H)
  • p. 208: multifractal model
  • pp. 227+ Ten Heresies of Finance
    1. Markets are turbulent
    2. Markets are very, very risky—more risky than the standard theories imagine
    3. Market timing matters greatly. Big gains and losses concentrate into small packages of time.
    4. Prices often leap, not glide. That adds to risk
    5. In markets, time is flexible
    6. Markets in all places and ages work alike
    7. Markets are inherently uncertain, and bubbles are inevitable
    8. Markets are deceptive
    9. Forecasting prices may be perilous, but you can estimate the odds of future volatility
    10. In financial markets, the idea of ‘Value’ has limited value
  • p. 253: Richard Olsen and Oanda.com
  • p. 259 Jean-Phillipe Bouchaud: multifractal/mean reversion + tail chiseeling by incorporating long tail hypothesis to avoid catastrophic risk
  • p. 263 fractal fingerprint

Some Mathematica fiddlings

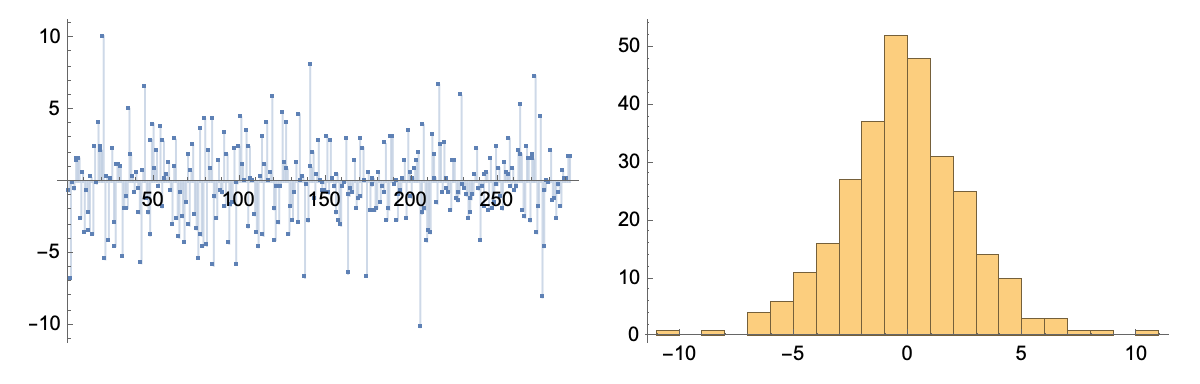
Pull stock prices and plot daily differences and see how it differs from the Browninan walk model but looks like a long tail distribution:

daily = FinancialData["NASDAQ:GOOG", {2022, 01, 01}]
With[
   {diff = Differences@daily["Values"]}, 
   {ListPlot[diff, Filling -> Axis], Histogram[diff]}] // GraphicsRow

13p2iv1p9mbra

19e9vbvr155i1

proc = EstimatedProcess[daily["Values"], GeometricBrownianMotionProcess[\[Mu], \[Sigma], S]]
path = RandomFunction[proc, {1, 293, 1}]
With[
   {diff = Differences@path["Values"]}, 
   {ListPlot[diff, Filling -> Axis], Histogram[diff]}] // GraphicsRow

(*GeometricBrownianMotionProcess[-0.00117877, 0.0247642, 145.074]*)

0wjgbilenpdqy

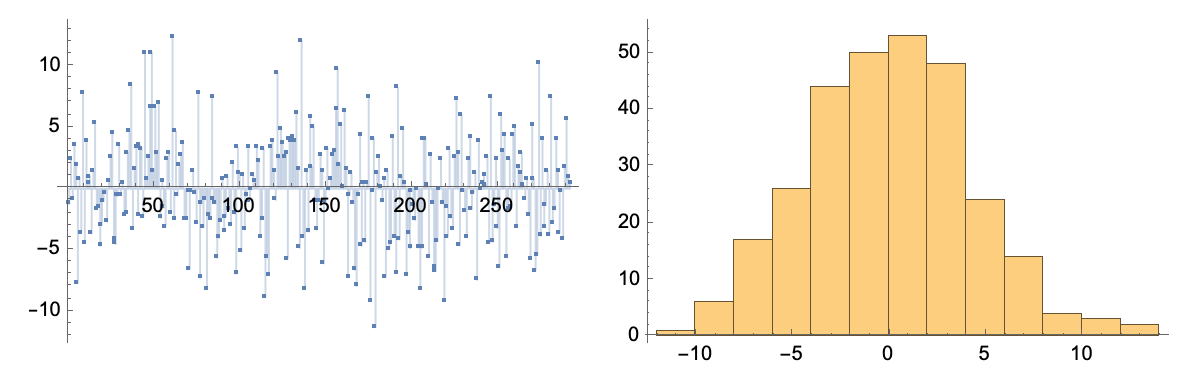
1ugxlmw43tzpd

I don’t know…looks like the Geometric Brownian motion is a pretty good description over this time period…

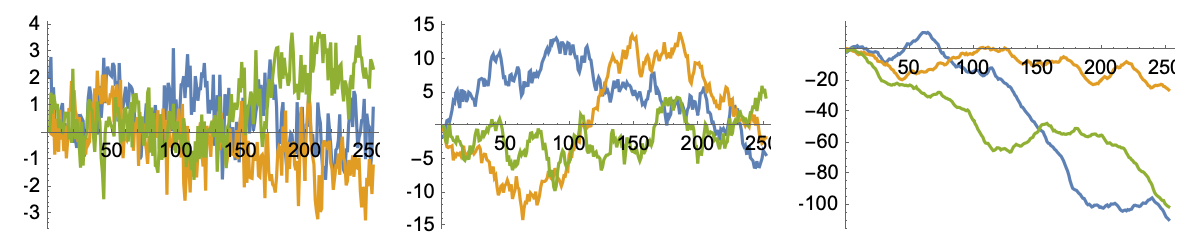
Reproduce figure with fraction brownian walk. H = 0.1, H=0.5, H=0.9

{low, med, high} = FractionalBrownianMotionProcess[0, 1, #] & /@ {0.1, 0.5, 0.9};
GraphicsRow@Map[ListLinePlot@RandomFunction[#, {1, 252, 1}, 3] &]@{low, med, high}

1czzvgagdh697

Further reading and resources / bibliographic extracts