Generating 3d-designs with OpenCASCADE Link

During the COVID-19 pandemic, I built a Prusa MK3S+ FDM 3d-printer from a kit. After printing the requisite pre-made objects, I started designing my own objects. Although I’ve more recently moved to doing a lot of work in Autodesk Fusion360 (I cranked through Kevin Kennedy’s youtube tutorial over Christmas break), it is always fun to do algorithmically-designed objects–especially since you are printing each object on-demand. My project here was to design a generative-designed mail caddy, where the size and placement of holes is completely random. By using circles, it can be printed without supports, while reducing the amount of filament. Also it looks cool. To do this, I used the OpenCASCADE Link in Mathematica…

Exterior shell

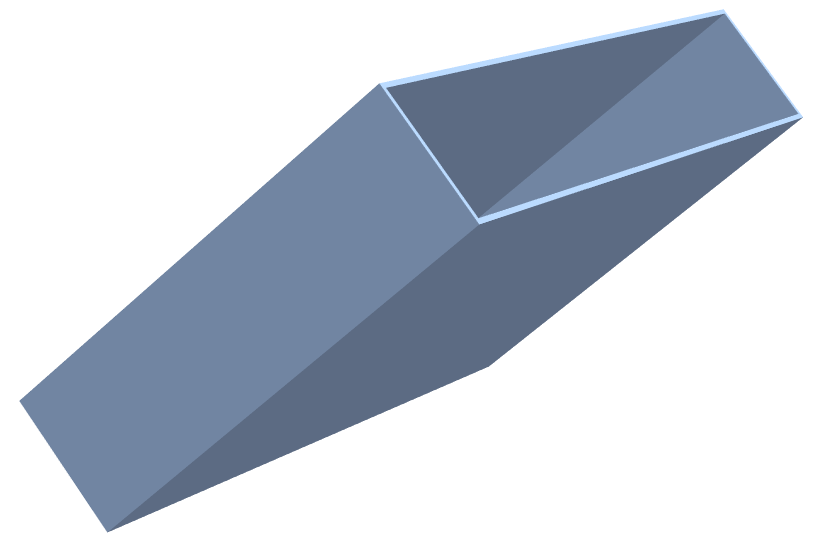
The underlying design idea to to create a simple shell and then create a tool that removes that shell. Here we make the shell.

h = 5.;
o = Sqrt[2]/2.;
w = 1.5;
t = 4./72; (*1.5 mm in inches as frame thickness*)
edge = 12./72; 
 
outer = Cuboid[{0, 0, 0}, {w, GoldenRatio*h, h}];
inner = Cuboid[{t, t, t}, {w - t, GoldenRatio*h - t, h*1.2}];

RegionDifference[outer, inner] // Region

Generate face punches

Now we define how to punch out the faces. I do this for each of the faces of the caddy independently.

fInside = Region@Cuboid[{edge, edge}, {GoldenRatio*h - edge, h - edge}]
fFrame = RegionDifference[Cuboid[{0, 0}, {GoldenRatio*h, h}], fInside]

(*warning: uses global variable t and edge*)
  Clear[holePuncher, maxDisk, punch] 
   
   maxDisk[{inside_, frame_}] := With[
     {center = RandomPoint[inside]}, 
     {center, RegionDistance[frame]@center}] 
   
   punch[{inside_, frame_, cuts_, status_}, center_, radius_, t_] := {RegionDifference[inside, Disk[center, radius]], RegionUnion[frame, Annulus[center, {radius - t, radius}]], 
     Append[cuts, {center, radius - t}], 
     status} 
   
   punch[{inside_, frame_, cuts_, status_}, center_, radius_, t_] := {RegionDifference[inside, Disk[center, radius]], RegionUnion[frame, Annulus[center, {radius - t, radius}]], 
     Append[cuts, {center, radius - t}], 
     status} 
   
   holePuncher[{inside_, frame_, cuts_, True}] := Module[
     {center, radius, nearest, maxRadius = 1.5, minRadius = 0.15, distanceFunction, 
      candidatePoints}, 
     
    (*define the distance function*) 
     distanceFunction = RegionDistance@BoundaryDiscretizeRegion[frame]; 
     
    (*distribute 1000 candidate points evenly throughout the area and evaluate distances to boundaries*) 
     candidatePoints = RandomPoint[inside, 1000]; 
     
    (*pick the one that allows us to draw the biggest circle*) 
     center = First@MaximalBy[candidatePoints, distanceFunction, 1]; 
     radius = Min[maxRadius, distanceFunction[center]]; 
     
     If[radius < minRadius, 
      {inside, frame, cuts, False}, 
     (*there is no place where we can fit an acceptable disk, so terminate*) 
     (*else*) 
     (*generate a suitable radius and randomly select a point that satisfies it*) 
      punch[{inside, frame, cuts, True}, center, radius, t] 
     ] (*endif*) 
    ] 
   
  (*when you can't punch any more holes, don't bother continuing*) 
   holePuncher[{inside_, frame_, cuts_, False}] := {inside, frame, cuts, False} 
   
   holePuncher[{inside_, frame_}] := holePuncher[{inside, frame, {}, True}] 
   
  (*convenience wrapper*) 
   holePuncher[{inside_, frame_}, iterations_Integer] := Nest[holePuncher, {inside, frame}, iterations] 
   
   holePuncher[{inside_, frame_, cuts_, status_}, iterations_Integer] := Nest[holePuncher, {inside, frame, cuts, status}, iterations] 
   
  

frontPattern = holePuncher[{fInside, fFrame}, 200];
frontPattern[[2]]

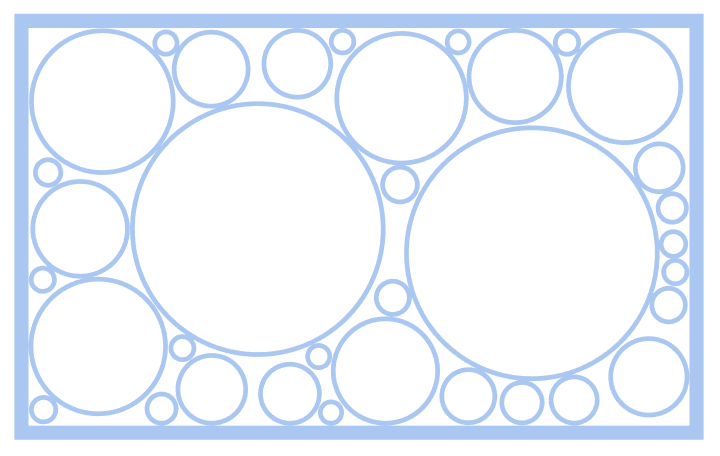
frontPattern // Last (*can we add moredisks?*)

(*False*)

Rear pattern should have holes punched…

hole1 = {1, h - 1};
hole2 = {h*GoldenRatio - 1, h - 1};

rearStart = punch[#, hole2, .5/2, .25/2] &@
     punch[#, hole1, .5/2, .25/2] &@{fInside, fFrame, {}, True}

rearPattern = holePuncher[rearStart, 200];
rearPattern[[2]]
Last[rearPattern]

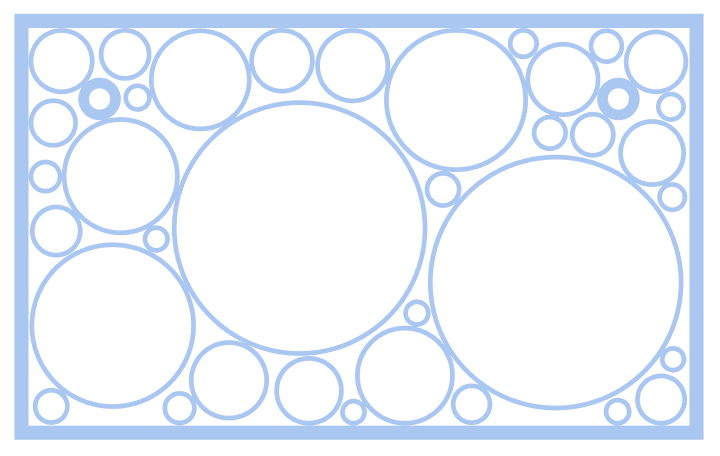
(*False*)

(*False*)

Sides

sInside = Region@Cuboid[{edge, edge}, {w - edge, h - edge}]
sFrame = RegionDifference[Cuboid[{0, 0}, {w, h}], sInside]

lSidePattern = holePuncher[{sInside, sFrame}, 50];
lSidePattern[[2]]
lSidePattern // Last

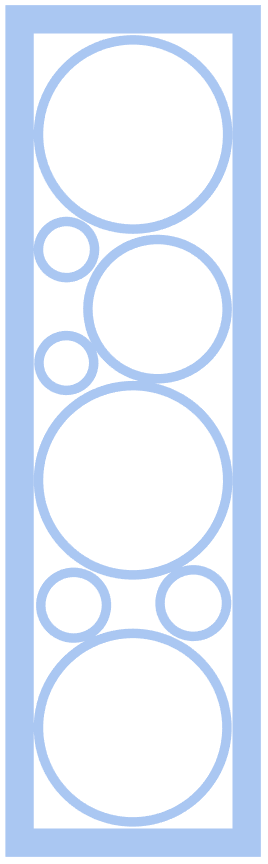
(*False*)

rSidePattern = holePuncher[{sInside, sFrame}, 50];
%[[2]]
%% // Last

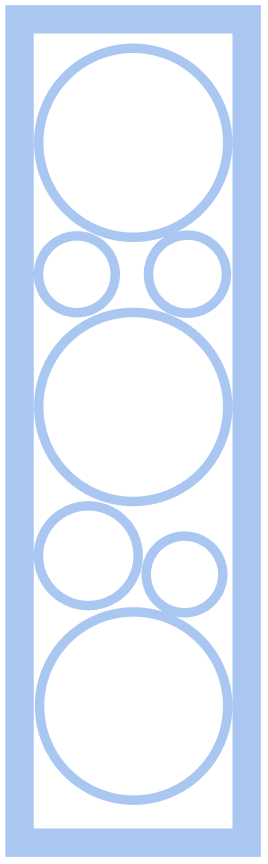
(*False*)

edge

(*0.166667*)

Bottom

bInside = Region@Cuboid[{edge, edge}, {w - edge, h*GoldenRatio - edge}];
bFrame = RegionDifference[Cuboid[{0, 0}, {w, h*GoldenRatio}], bInside];
bPattern = holePuncher[{bInside, bFrame}, 50];
%[[2]]
%% // Last

(*False*)

Create Cylinder objects

cylindrizeFront[res_, xMin_, xMax_] := 
   RegionUnion @@ MapThread[
     Cylinder[{ Prepend[xMin]@#1, Prepend[xMax]@#1}, #2] &, 
     Transpose[res]] 
 
cylindrizeSide[res_, xMin_, xMax_] := 
   RegionUnion @@ MapThread[
     Cylinder[{ {#1[[1]], xMin, #1[[2]]}, {#1[[1]], xMax, #1[[2]]}}, #2] &, 
     Transpose[res]] 
 
cylindrizeBottom[res_, xMin_, xMax_] := 
   RegionUnion @@ MapThread[
     Cylinder[{ {#1[[1]], #1[[2]], xMin}, {#1[[1]], #1[[2]], xMax}}, #2] &, 
     Transpose[res]] 
 
Region[
  cuts = RegionUnion[
    cylindrizeFront[frontPattern[[3]], w/2, w + 1], 
    cylindrizeFront[rearPattern[[3]], w/2, -1], 
    cylindrizeSide[lSidePattern[[3]], -1, 1], 
    cylindrizeSide[rSidePattern[[3]], h*GoldenRatio + 1, h*GoldenRatio - 1], 
    cylindrizeBottom[bPattern[[3]], -1, 1], 
    inner 
   ]]

Process using OpenCASCADE

Using default Mathematica objects tends to crash with very complicated object intersections and differences. However, the OpenCASCADE Link module makes it easy to do the underlying processes in OpenCASCADE, an industrial-strength open-source computational geometry package.

Needs["OpenCascadeLink`"]

u = OpenCascadeShapeUnion[ OpenCascadeShape /@ cuts[[2]]];
o = OpenCascadeShape[outer]; 
 
d = OpenCascadeShapeDifference[o, u]

(*OpenCascadeShapeExpression[209]*)

OpenCascadeShapeSurfaceMeshToBoundaryMesh[d]["Wireframe"]

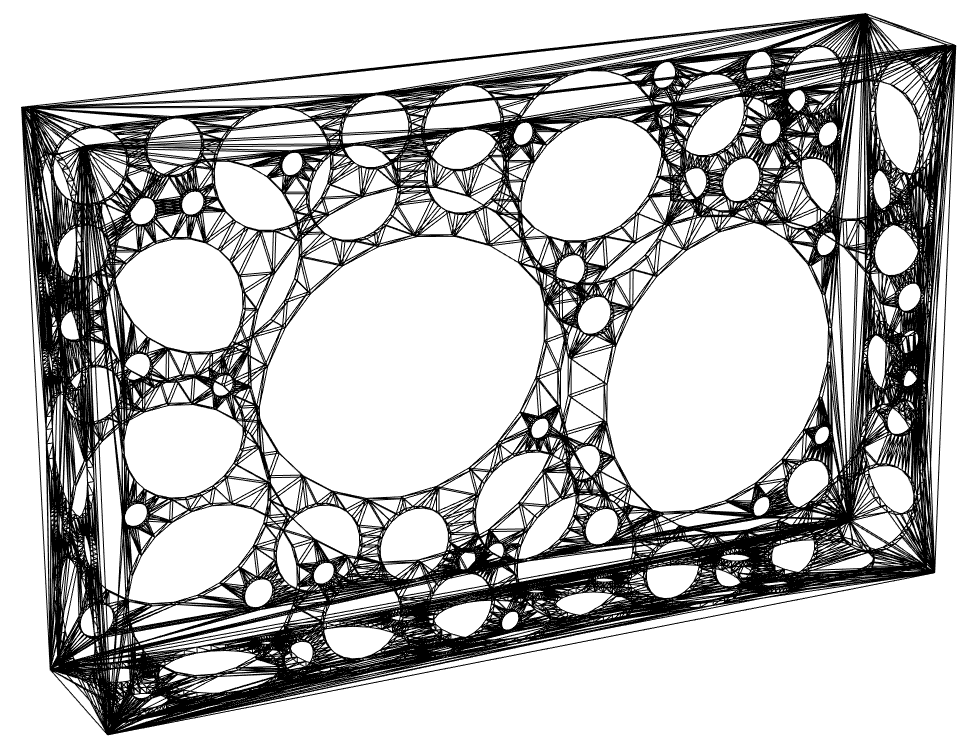
Now that we’re happy, we can export an STL file which can be imported into your favorite slicer program:

OpenCascadeShapeExport["caddy.stl", d] (*export it for printing*)
Import["caddy.stl"] (*re import the exported STL to visualize*)

(*"caddy.stl"*)

If you pull this into your slicer program, you’ll find that this design requires: 46.91 g of filament, 4h:4m print time at 0.3mm resolution. (An earlier version of this program, v2 caddy which required 60g of filament…the difference here is that we fill the holes in more effectively).

(I printed one of these…and it continues to store mail 1.5 years later)

NotebookFileName@EvaluationNotebook[]
ToJekyll["Generating 3d-designs with OpenCASCADE Link", "3dprinting opencascade"];

(*"/Users/jschrier/Dropbox/journals/3dprinting/2021.05.11_caddy_v3.nb"*)