Von Neumann Poker

In Von Neumann poker, each player picks a random uniform variable X & Y drawn from [0,1]. Each player pays an ante of $1. Whoever has the higher hand wins. Each player sees only his own hand. What’s the optimal betting (and bluffing) strategy?

Player I can either call (reveal cards) ending the game or raise by a predetermined amount $B.

If raised, then Player II can either fold (losing the $1 ante) or check the bet (matching the $B). Then whoever wins, wins.

The strategy is as follows. Player 1 will bluff if x < a and raise if x>b. Player 2 will fold if Y <c.

What is the optimal (stable) strategy?

Approach: View the problem geometrically and work out the areas of the different payout (for player I) as follows (because it is a zero sum game, anytime play I wins some reward p, Player II wins -p).

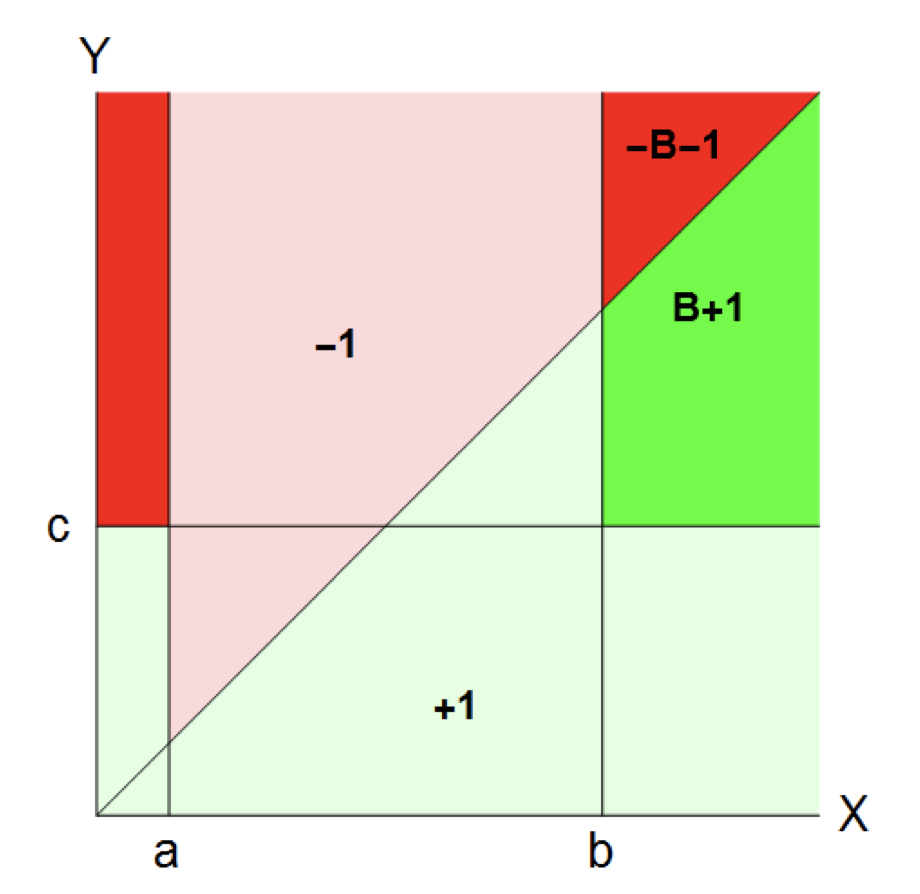
Clear[p, a, b, c, B] 
 
p = (+1)*((b^2/2) + (1 - b) c + (a*c - a^2/2)) + 
   (B + 1)*( (1 - b )*(1 - c) - (1 - b)^2/2) + 
   (-B - 1)*(( a*(1 - c) + (1 - b)^2/2))  + 
   (-1)*( (1 - a)^2/2 - (1 - b)^2/2)

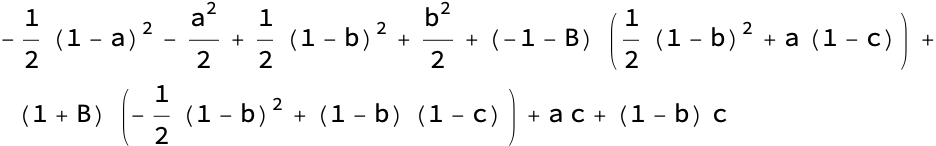
Either player can change strategy, so we are looking for a local maximum (from the perspective of player 1) or a local minimum (from the perspective of player 2); if there were multiple extrema, we would have to find them and evaluate, however there is only one unique strategy for both players, which we can find by setting the derivatives equal to zero and solving for the parameters:

soln = Solve[
    D[p, a] == 0 && D[p, b] == 0 && D[p, c] == 0, {a, b, c}] // Factor

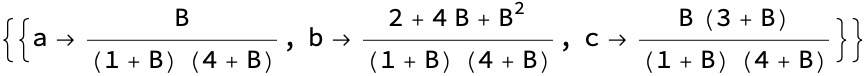
(In agreement with known results from (https://faculty.math.illinois.edu/~hildebr/ugresearch/HildebrandCalculusSpring2017-report.pdf) , which is also the source of the figure above)

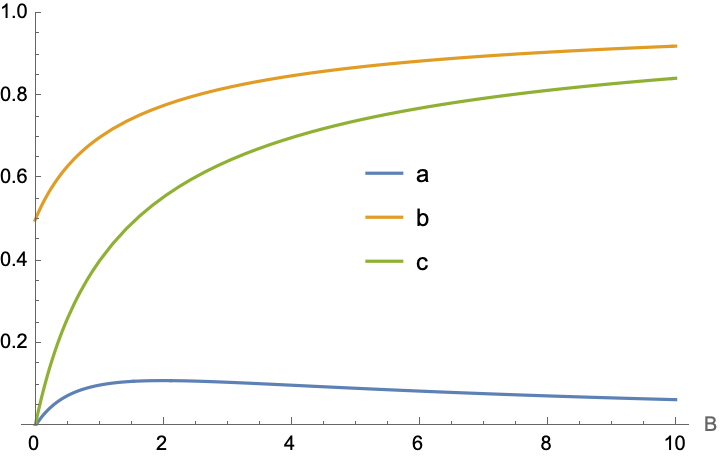
How do the strategies change as the bet size, B, increases?

With[
  {f = Association@First[soln]}, 
  Plot[
   {f[a] /. B -> x, f[b] /. B -> x, f[c] /. B -> x}, 
   {x, 0, 10}, 
   PlotLegends -> Placed[{"a", "b", "c"}, {Center, Right}], 
   AxesLabel -> {"B"}, PlotRange -> {All, {0, 1}} 
  ]]

What is the expected value for Player 1 under optimal play for both players as a function of the bet size, B?

Plot[
  p /. soln /. B -> x, {x, 0, 10}, 
  AxesLabel -> {"B", "Expected value for Player 1"}]

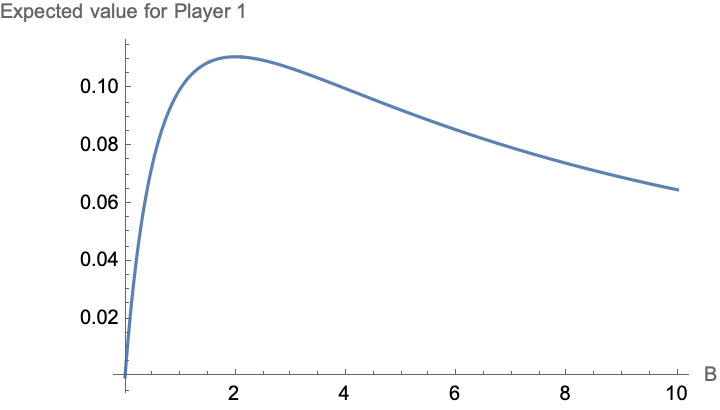
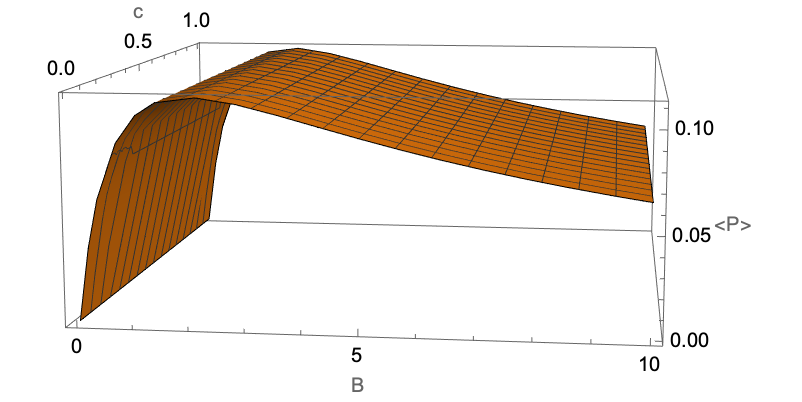
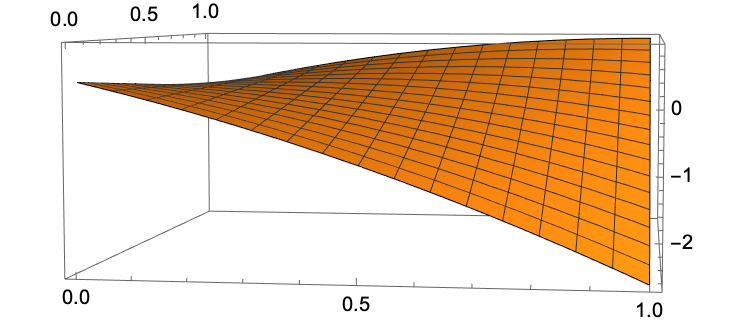
An interesting property is that if Player I adopts this strategy, then the payoff is fixed regardless of Player II is choice:

Plot3D[
  (p /. soln[[1, 1 ;; 2]] /. {B -> x, c -> y}), 
  {x, 0, 10}, {y, 0, 1}, AxesLabel -> {"B", "c", "<P>"}]

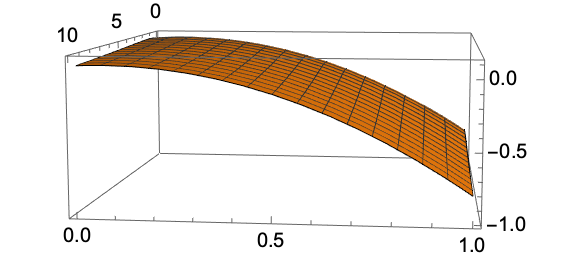
Suppose Player II sticks with his optimal strategy, but Player I chooses the bluffing threshold incorrectly (wrong a):

Plot3D[
  (p /. soln[[1, 2 ;; 3]] /. {B -> x, a -> y}), 
  {x, 0, 10}, {y, 0, 1}]

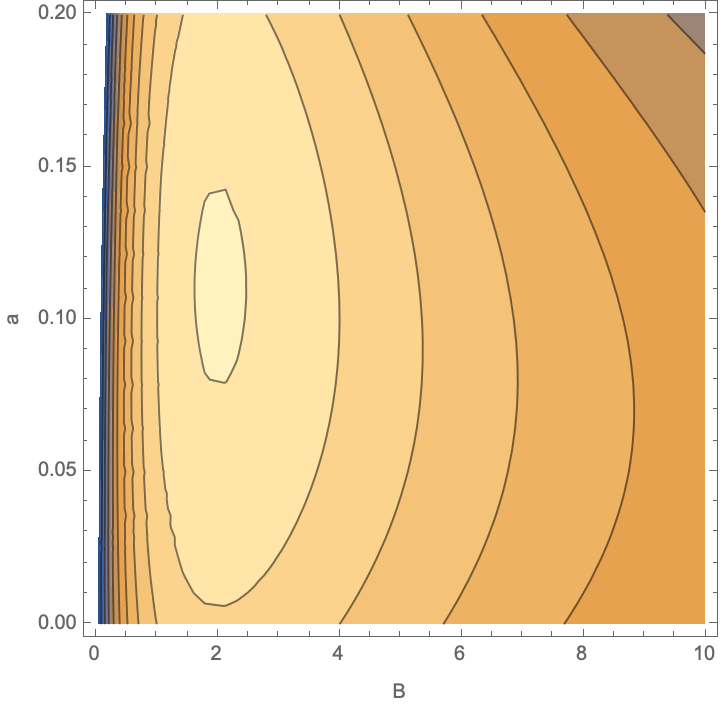
ContourPlot[
  (p /. soln[[1, 2 ;; 3]] /. {B -> x, a -> y}), 
  {x, 0, 10}, {y, 0, 0.2}, FrameLabel -> {"B", "a"}]

Plot[(p /. soln[[1, 2 ;; 3]] /. {B -> 1, a -> y}), {y, 0, 1}]

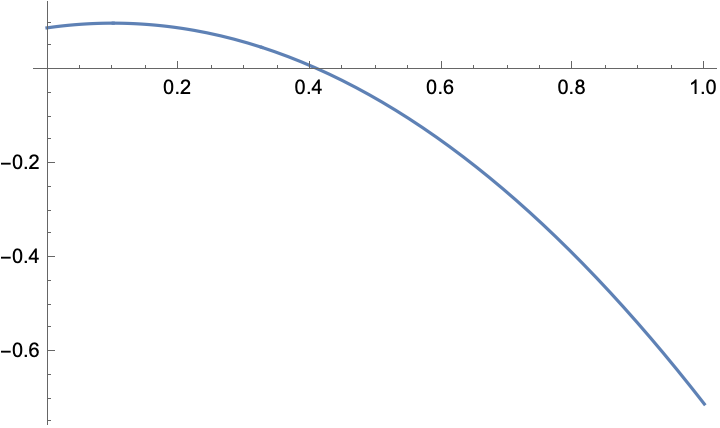
Another version: Suppose II knows how Player I is suboptimal bluff (wrong values of a)…can II take advantage of this?

Plot3D[
  (p /. soln[[1, 2]] /. {B -> 2, a -> x, c -> y}), 
  {x, 0, 1}, {y, 0, 1} 
 ]

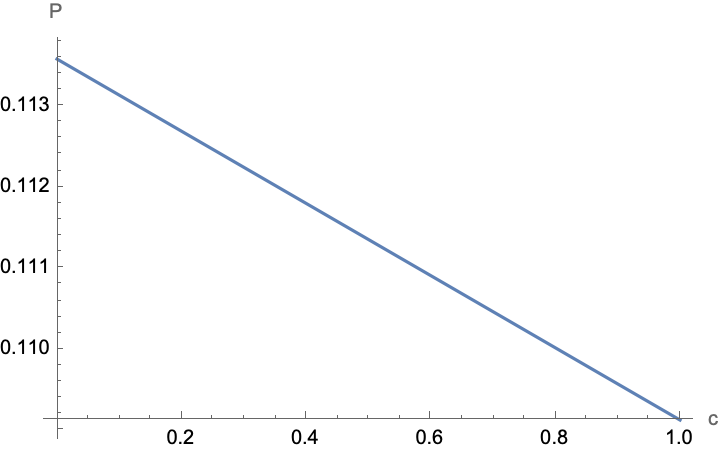
If I plays close to optimal, there is no way for II to win:

Plot[(p /. soln[[1, 2]] /. {B -> 2, a -> 0.11, c -> y}), {y, 0, 1}, 
  AxesLabel -> {"c", "P"}]

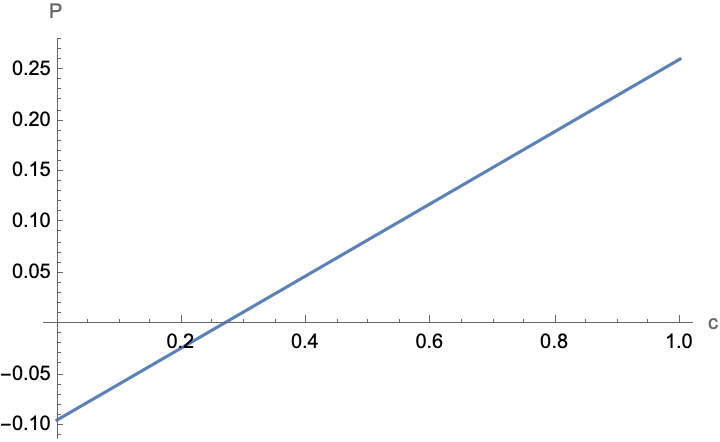
But if I plays suboptimally, then II can find a choice for c to exploit this (negative expected value from the perspective of I):

Plot[(p /. soln[[1, 2]] /. {B -> 2, a -> 0.2, c -> y}), {y, 0, 1}, 
  AxesLabel -> {"c", "P"}]

How “good” or “bad” can this be: Let is try to find the minimum value (best case for II)

Plot[
  MinValue[
   {(p /. soln[[1, 2]] /. {B -> 2, a -> x}), 0 <= c <= 1}, c], 
  {x, 0, 1}, AxesLabel -> {"a", "P (optimal c for II)"}]

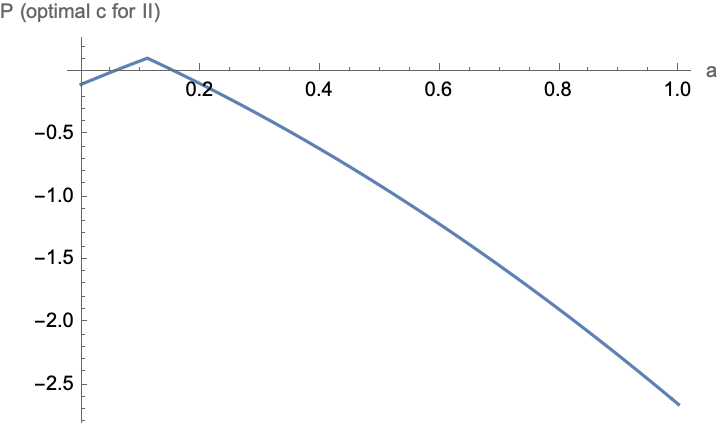
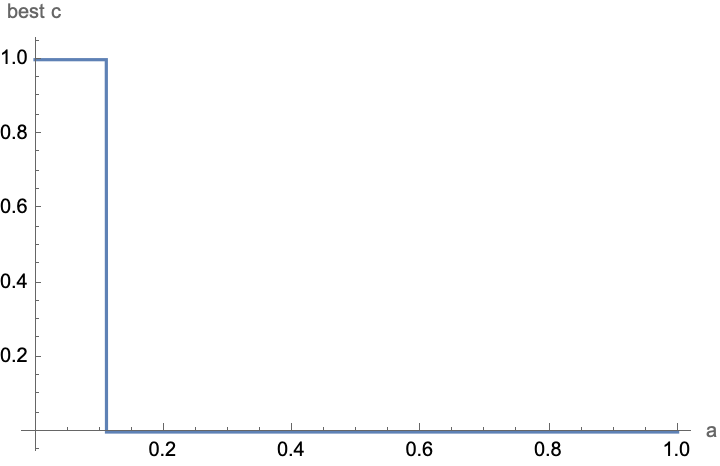
In practice this looks pretty simple: If we know that a is less than the optimal choice, then set c high; if we know that a is greater than the optimal choice, then set c low, and when optimal, play the optimal strategy:

Plot[
  ArgMin[
   {(p /. soln[[1, 2]] /. {B -> 2, a -> x}), 0 <= c <= 1}, c], 
  {x, 0, 1}, AxesLabel -> {"a", "best c"}]

NotebookFileName@EvaluationNotebook[]
ToJekyll["Von Neumann Poker", "game-theory optimization geometry gambling"];

(*"/Users/jschrier/Dropbox/journals/mathematica/2022.01.29_von_neumann_poker.nb"*)